Законы Гиббса-Коновалова

Законы Гиббса-Коновалова (1881 г.) установливают соотношения между составами равновесных жидких растворов и составами их паров, а также общим давлением насыщенного пара над ними.

Первый закон Гиббса-Коновалова гласит: в насыщенном паре над раствором преобладает по сравнению с раствором тот компонент, добавление которого к раствору приводит к возрастанию общего давления насыщенного пара (пар обогащен легколетучим компонентом). Данный закон выполняется для любых растворов, а на рассматриваемом явлении основана фракционная перегонка (ректификация), позволяющая разделить смесь взаимно-растворимых жидкостей.

Докажем первый закон Гиббса-Коновалова, для чего воспользуемся уравнением Дюгема-Маргулеса (8.10), устанавливающим связь между изменениями парциальных давлений пара компонентов и составом раствора при постоянных температуре и давлении. В расчете на 1 моль жидкого бинарного раствора указанное уравнение принимает вид

.

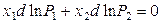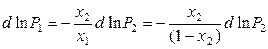. (8.35)

Преобразуем уравнение (8.35):

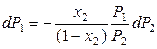. (8.36)

Учтем, что

, ,

тогда

. (8.37)

Поскольку

, ,

то

. (8.38)

Разделим правую и левую части уравнения (8.38) на dx ₂, получим:

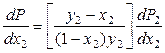. (8.39)

Поскольку производная (dP ₂/ dx ₂) > 0 (парциальное давление второго компонента в паре увеличивается с ростом его мольной доли в растворе), то знак производной (dP / dx ₂) определяется знаком разности (y ₂ – x ₂). Если y ₂ > x ₂, то (dP / dx ₂) > 0, что и требовалось доказать.

С учетом вышеизложенного первый закон Гиббса-Коновалова может быть сформулирован и так: общее давление пара над раствором растёт с ростом доли в растворе того компонента, который богаче представлен в паре (более летучего компонента).

Второй закон Гиббса-Коновалова касается более частных случаев и выполняется для реальных растворов с большими отклонениями от закона Рауля, на кривых «общее давление пара – состав» для которых имеются минимумы или максимумы. Второй закон Гиббса-Коновалова гласит: максимум на кривой общего давления соответствует минимуму на кривой температур кипения и отвечает такому равновесию раствора и насыщенного пара, при котором составы фаз одинаковы, и наоборот.

Экстремумы на кривой зависимости общего давления насыщенного пара от состава раствора удовлетворяют условию (dP / dx ₂) = 0, а в соответствии с уравнением (8.39) это возможно, только если в этих точках y ₂ = x ₂. Итак, в экстремумах общего давления пара (или температур кипения) раствор и насыщенный пар имеют одинаковый состав.

Возможные диаграммы состояния бинарных систем с максимумом на кривой давления пара и минимумом на кривой температур кипения представлены на рис. 8.7.

Рис. 8.7. Диаграммы состояния бинарных систем с максимумом на кривой давления пара (а) и минимумом на кривой температур кипения (б).

Смеси, у которых раствор и пар одинаковы по составу, называются азеотропными, или нераздельнокипящими. Путём перегонки азеотропные растворы не разделяются (составы фаз равны). Но их можно разделить следующими методами:

— путём химического связывания одного из компонентов;

— путем добавления в систему третьего компонента;

— путем ректификации на двух последовательных колонках при различных давлениях.

Примерами азеотропных смесей с минимумами на кривых температур кипения являются растворы, содержащие Н₂О и С₂Н₅ОН (96,5%), метанол и ацетон. Примерами азеотропных смесей с максимумами на кривых кипения являются растворы, содержащие Н₂О и НСl (20%), ацетон и хлороформ.

Третий закон Гиббса-Коновалова гласит: в изотермических или изобарических условиях состав насыщенного пара и состав жидкого раствора меняются синбатно (составы обеих фаз меняются в одном направлении). Данный закон логично следует из изученного материала и для его обоснования достаточно еще раз внимательно изучить диаграммы состояния, представленные, например, на рис. 8.3 – 8.5.

Дата добавления: 2014-01-04