
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Активность
|
|
|
|
Химический потенциал компонента в реальном растворе.
Итак, уравнение (8.42)
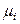 (р-р) =
(р-р) = 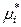 (ж) +
(ж) + 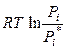
справедливо как для идеальных, так и для реальных растворов.
Химические потенциалы компонентов в идеальных растворах определяется соотношением
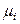 (р-р) =
(р-р) = 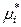 (ж) +
(ж) +  ,
,
а химические потенциалы растворителя и растворенного вещества в предельно разбавленных реальных растворах – соотношениями
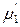 (р-р) =
(р-р) = 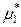 (ж) +
(ж) +  .
.
 (р-р) =
(р-р) = 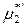 (ж) +
(ж) + 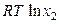 .
.
Возникает вопрос: а как определить химический потенциал компонентов в реальных растворах при произвольных концентрациях веществ (исключая область бесконечно разбавленных растворов)? Закон Рауля для таких неидеальных растворов не выполняется. Однако можно ожидать, что для реальных растворов отношение
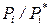
будет играть ту же роль, что и мольная доля компонента xi в уравнениях для идеальных растворов.
Законы идеальных растворов будут формально выполняться для реальных растворов, если заменить в термодинамических выражениях мольную долю новой термодинамической функцией, впервые введенной Льюисом и названной термодинамической активностью. Термодинамическая активность ai – это функция, которая при подстановке в формулу для химического потенциала идеального раствора дает правильное значение химического потенциала компонента в реальном растворе:
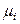 (р-р) =
(р-р) = 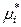 (ж) +
(ж) + 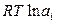 , (8.46)
, (8.46)
Поскольку из уравнений (8.42) и (8.46) следует, что
 ,
,
то активность компонента в реальном растворе с мольной долей xi может быть определена на основе измерений парциального давления пара компонента над раствором и давления насыщенного пара над чистым веществом при заданной температуре. В общем случае активность компонента является функцией температуры, давления и мольной доли (состава).
Можно дать и такое определение: активность компонента – это такая концентрация данного компонента в идеальном растворе, при которой он в последнем имеет такой же химический потенциал, что и в реальном растворе (рис. 8.8). Новая функция состояния – активность – не раскрывает причин отклонения данного раствора от идеального поведения, зато упрощает формальное математическое описание термодинамически неидеальных растворов.
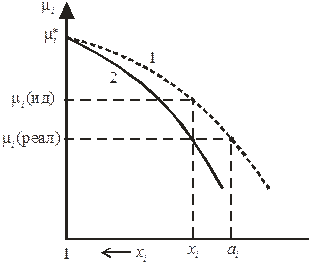
Рис. 8.8. Зависимость химического потенциала компонента от концентрации
в идеальном (кривая 1) и реальном (кривая 2) растворе.
Для характеристики степени отклонения реального раствора от идеального в термодинамике вводится коэффициент активности:
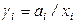 ,
,  .
.
Поскольку химический потенциал i -го компонента в идеальном и реальном растворах определяется выражениями
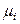 (ид.) =
(ид.) = 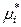 (ж) +
(ж) +  и
и 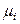 (реал.) =
(реал.) = 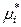 (ж) +
(ж) + 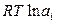
соответственно, то его изменение при переходе от идеального к реальному раствору равно
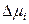 =
= 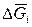 =
=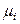 (реал.) –
(реал.) – 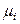 (ид.) =
(ид.) = 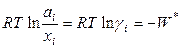 .
.
Величина
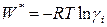
представляет собой работу переноса 1 моля i -го компонента из идеального раствора в данный реальный раствор.
Коэффициент активности (как и активность) является функцией не только температуры и давления, но и концентрации. Поэтому при определении активности и коэффициента активности компонентов реальных растворов существенным является выбор стандартного состояния.
В общем случае для компонентов реальных растворов (жидких и твердых тел) справедливо следующее выражение:
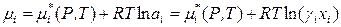 , (8.47)
, (8.47)
где величина
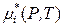
является химическим потенциалом i -го компонента в стандартном состоянии (химическим потенциалом при ai = 1).
Чтобы полностью определить коэффициент активности (и активность), необходимо указать условия, при которых он становится равным единице. Сделать это можно двумя способами, так как при xi → 1 зависимость парциального давления пара i -го компонента от состава стремится к закону Рауля, а при xi → 0 – к закону Генри.
Численно сравнивать химические потенциалы вещества можно только при условии, что они отнесены к одному и тому же стандартному состоянию.
В настоящее время используют два способа выбора стандартного состояния: симметричный и несимметричный.
1). При симметричном способе за стандартное состояние каждого компонента принимается состояние чистого вещества и в этом состоянии активность каждого компонента принимается равной единице; соответственно и коэффициент активности в стандартном состоянии равен единице:
 ,
, 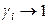 при
при  .
.
При симметричном способе выбора стандартного состояния химический потенциал компонента в стандартном состоянии равен мольной энергии Гиббса чистого компонента при данных температуре и давлении:
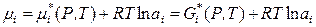 ,
,
Данный метод применяется обычно при изучении растворов неэлектролитов, когда компоненты неограниченно растворимы друг в друге.
2). При несимметричном способе за стандартное состояние компонентов принимаются их состояния в бесконечно разбавленном растворе. В этих условиях растворитель подчиняется закону Рауля и за стандартное состояние растворителя принимается состояние чистого вещества:
для растворителя:  ,
, 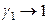 при
при 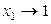 ;
;
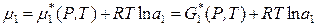 .
.
Давление пара растворенного вещества подчиняется закону Генри и за стандартное состояние растворенного вещества принимается его состояние в бесконечно разбавленном растворе: коэффициент активности приближается к единице, когда концентрация приближается к нулю:
для растворенного вещества: 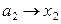 ,
, 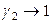 при
при 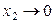 .
.
Несимметричный способ используется при ограниченной растворимости компонентов (если мольные доли некоторых компонентов не могут быть изменены вплоть до единицы), например, для жидких растворов твердых веществ и газов.
Если коэффициент активности растворенного вещества приближается к единице при бесконечном разбавлении, то в уравнении
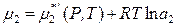
величина
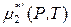
представляет собой химический потенциал чистого растворенного вещества в гипотетическом состоянии. В этом гипотетическом состоянии вещество с активностью, равной единице, обладает свойствами, характерными для бесконечно разбавленного раствора (выполняется закон Генри). Поэтому давление насыщенного пара чистого вещества в таком гипотетическом состоянии равно не  , а константе Генри k 2.
, а константе Генри k 2.
В растворе любой концентрации выполняются соотношения
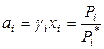 ,
,  . (8.48)
. (8.48)
Тогда для бинарного раствора коэффициенты активности растворителя и растворенного вещества при симметричном выборе стандартного состояния определяются выражениями
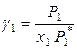 и
и 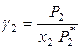 , (8.49)
, (8.49)
а при несимметричном выборе стандартного состояния – выражениями
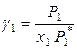 и
и 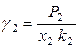 . (8.50)
. (8.50)
Итак, численные значения коэффиентов активности растворителя не зависят от способа выбора стандартного состояния, а растворенного вещества – зависят. Рассмотрим в качестве примера раствор брома в четыреххлористом углероде при 25 oC, для которого
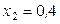 ;
; 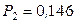 атм;
атм; 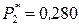 атм;
атм;  атм.
атм.
Вычислим коээфициент активности и активность брома в растворе при симметричном и несимметричном выборе стандартного состояния:
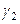 (симм.)
(симм.) 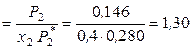 ,
, 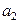 (симм.)
(симм.) 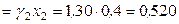 ;
;
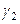 (несимм.)
(несимм.) 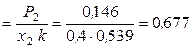 ,
, 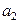 (несимм.)
(несимм.)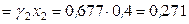 .
.
Следует отметить, что при симметричном выборе стандартного состояния с учетом выражений (8.48) и (8.49) для растворов с положительными отклонениями от идеальности: γi > 1, ai > xi; а для растворов с отрицательными отклонениями от идеальности: γi < 1, ai < xi.
В заключение следует добавить, что кроме рассмотренного в данном разделе рационального коэффициента активности
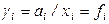 ,
,
в термодинамике используются еще практический
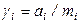 (где mi – моляльность раствора)
(где mi – моляльность раствора)
и молярный
 (где Сi – молярность раствора)
(где Сi – молярность раствора)
коэффициенты активности.
Дополнительный материал.
Доказажем справедливость соотношений (8.49) и (8.50). Для пара (идеальный газ) и раствора, находящихся в равновесии, справедливо:
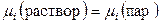 ,
,
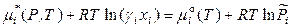 ,
,
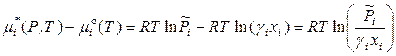 ,
,
 . (8.51)
. (8.51)
Проанализируем уравнение (8.51):
1). При симметричном способе выбора стандартного состояния
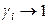 при
при 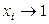 (чистое вещество),
(чистое вещество),
тогда

и при любых составах раствора
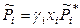 ,
,  ,
,  . (8.52)
. (8.52)
При коэффициентах активности, равных 1, выражения (8.52) переходят в закон Рауля.
2). При несимметричном способе выбора стандартного состояния для растворителя выполняются соотношения (8.52), а для растворенного вещества справедливо:
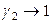 при
при 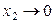 (предельно разбавленный раствор),
(предельно разбавленный раствор),
тогда
 ,
, 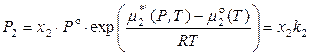 ,
,
 .
.
Следовательно, при любых составах раствора
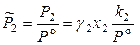 ,
,  ,
,  . (8.53)
. (8.53)
При коэффициенте активности растворенного вещества, равном 1, выражения (8.53) переходят в закон Генри.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 3209; Нарушение авторских прав?; Мы поможем в написании вашей работы!