
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
И предельно разбавленном жидком растворе
|
|
|
|
Химический потенциал компонента в идеальном
Если раствор находится в равновесии с паром (насыщенным), то химические потенциалы компонентов в паре и жидкости одинаковы (условие равновесия в гетерогенной многокомпонентной системе):
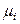 (р-р) =
(р-р) = 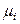 (пар),
(пар),
где μi (р-р) – химический потенциал i -го компонента в жидком растворе; μi (пар) – химический потенциал i -го компонента в паре над раствором.
Если рассматривать пар как смесь идеальных газов, то
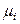 (р-р) =
(р-р) = 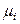 (г) =
(г) = 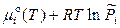 , (8.40)
, (8.40)
где  – относительное парциальное давление пара i -го компонента.
– относительное парциальное давление пара i -го компонента.
При равновесии чистого жидкого i -го компонента с его насыщенным паром справедливо:
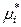 (ж) =
(ж) = 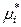 (г) =
(г) =  , (8.41)
, (8.41)
где 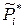 – относительное давление пара над чистым i -м компонентом.
– относительное давление пара над чистым i -м компонентом.
Вычитая уравнение (8.41) из уравнения (8.40), получаем
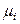 (р-р) =
(р-р) = 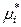 (ж) +
(ж) + 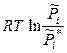 =
= 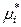 (ж) +
(ж) + 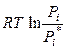 . (8.42)
. (8.42)
В последнем уравнении химический потенциал i -го компонента в растворе выражен через химический потенциал чистого i -го компонента (молярную энергию Гиббса) и отношение давлений насыщенного пара компонента над раствором и над чистой жидкостью при той же температуре. Выражение (8.42) справедливо для любых жидких растворов, поскольку при его выводе не сделано никаких предположений относительно характера раствора.
Если жидкий раствор является идеальным, то по закону Рауля
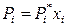 ,
, 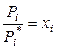 ,
,
следовательно,
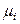 (р-р) =
(р-р) = 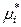 (ж) +
(ж) +  . (8.43)
. (8.43)
Полученное уравнение может служить определением идеального раствора как раствора, химический потенциал каждого компонента которого при данных температуре и давлении определяется уравнением (8.43).
В случае реальных предельно разбавленных растворов растворитель подчиняется закону Рауля, а растворенное вещество – закону Генри:
 .
.
Поэтому химический потенциал растворителя в предельно разбавленном реальном растворе определяется уравнением
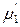 (р-р) =
(р-р) = 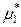 (ж) +
(ж) +  . (8.44)
. (8.44)
(Верхний штрих указывает на бесконечно разбавленный раствор).
Для растворенного вещества в предельно разбавленном реальном растворе уравнение (8.42) запишется в виде:
 (р-р) =
(р-р) =  (ж) +
(ж) + 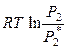 =
=  (ж) +
(ж) + 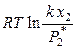 ,
,
 (р-р) = [
(р-р) = [ (ж) +
(ж) +  ] +
] + 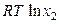 ,
,
 (р-р) =
(р-р) = 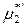 (ж) +
(ж) + 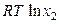 , (8.45)
, (8.45)
где
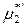 (ж) =
(ж) =  (ж) +
(ж) +  .
.
При отрицательных отклонениях от закона Рауля
 и
и 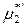 (ж) <
(ж) <  (ж);
(ж);
при положительных отклонениях от закона Рауля
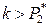 и
и 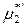 (ж) >
(ж) >  (ж).
(ж).
Следует помнить, что химический потенциал i -го компонента в растворе всегда меньше химического потенциала чистого компонента. Слагаемое RT ln xi как раз и отражает изменение химического потенциала компонента при образовании раствора.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1285; Нарушение авторских прав?; Мы поможем в написании вашей работы!