Напряжения изгиба и суммарные напряжения

Напряжения изгиба от действия газовых и центробежных сил определяются раздельно, а затем алгебраическим суммированием определяются суммарные напряжения изгиба. Такое вычисление напряжений облегчает определение наиболее опасных условий работы лопатки.

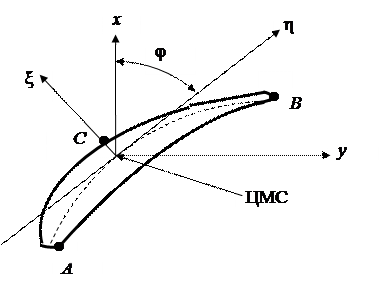
Напряжения изгиба определяются по изгибающим моментам относительно главных центральных осей сечения лопатки. Методика определения положения главных центральных осей излагается в курсе сопротивления материалов. Начало координат новой системы располагается в центре масс сечения. Координаты центра масс сечения от носка и от хорды профиля можно определить приближенно по эмпирическим формулам:

, ,

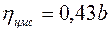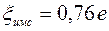где 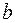– хорда профиля; 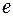– максимальный прогиб линии профиля.

Для большинства современных профилей допустимо считать ось 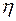направленной параллельно хорде профиля (погрешность не превышает 3…4⁰), ось 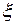перпендикулярна оси 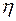, новая система координат повернута относительно прежней системы на угол .

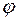Проекции векторов изгибающих моментов от газовых или центробежных сил в новой системе координат имеют вид:

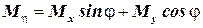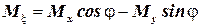, – для компрессора;

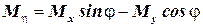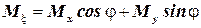, – для турбины.

Напряжения изгиба в произвольной точке поперечного сечения профиля с координатам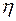и и 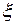при косом изгибе определяются по формуле:

,

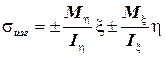где 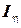и 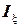– моменты инерции сечения профиля относительно главных центральных осей. Значения изгибающих моментов 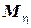и 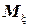и координат 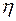и 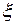подставляются со своими знаками.

Величины моментов инерции можно определить приближенно по эмпирическим формулам:

, ,

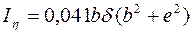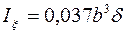где 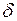– максимальная толщина профиля.

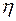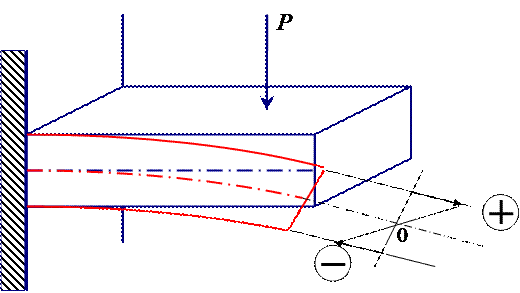
Напряжения изгиба определяются обычно для трех характерных точек профиля, наиболее удаленных от нейтральных осей и 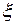(на нейтральных осях напряжения изгиба равны нулю). В этих точках напряжения изгиба будут максимальными. Наиболее опасные точки располагаются на носке, хвостике и спинке профиля (точки А, В и С).

			Типичная задача из Сопромата: при изгибе балки максимальные напряжения растяжения – на растянутых волокнах, максимальные напряжения сжатия – на сжатых волокнах, а на нейтральной оси - нулевые напряжения

Напряжения изгиба в точках, наиболее удаленных от нейтральных осей, будут равны:

.

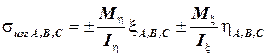Суммарные напряжения в точках А,В и С с учетом напряжений растяжения от действия центробежных сил определяются алгебраическим суммированием напряжений растяжения и напряжений изгиба от газовых и центробежных сил:

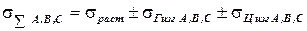
(напряжения 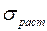всегда положительны, а напряжения 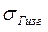и 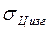необходимо подставлять со своими знаками: «+» – при растяжении и «–» – при сжатии.

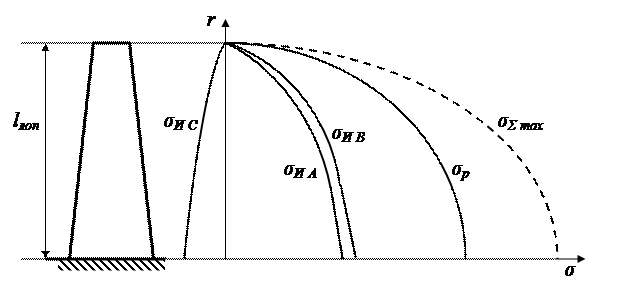На рис. представлен примерный характер изменения напряжений растяжения, изгиба и суммарных напряжений по длине лопатки.

Дата добавления: 2014-01-04