Тема 6.1 Принцип метода математической индукции

Индукцией называется метод ведущий от частных примеров к некоторому общему выводу.

Будем складывать нечетные числа:

- называется гипотезой (или предположением).

Гипотеза может быть либо истинной, либо ложной - это доказывается методом математической индукции, то есть заключается в следующем:

1. Проверить: А(n) - гипотеза

При n=1 – гипотеза выполняется: А(1) – верно.

2. Допустим, что при n=k, А(k) – верно.

Взять n=k+1 и доказать, что А(k+1) – верно, используя пункт 2.

Замечание. Чтобы показать, что эта формулировка следует из предыдущей, достаточно рассмотреть множество A={x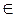N | P верно для x}.

Для доказательства в обратную сторону, множеству A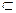N можно сопоставить свойство P «быть элементом множества A».

О доказательствах, основанных на аксиоме индукции, говорят, что они проведены методом математической индукции. Такие доказательства имеют следующую структуру:

- устанавливается справедливость P для n=0 (посылка индукции);

- предполагается, что P справедливо для некоторого произвольного, но фиксированного n=k (индуктивное предположение);

- доказывается, что из индуктивного предположения, следует, что P верно для n=k+1 (индуктивный шаг).

Примеры.Проведем два доказательства методом математической индукции.

1) Сумма первых натуральных чисел от 0 до n включительно равна 0,5n(n+1):

0+1+…+n = 0,5n(n+1).

Доказательство. Утверждение верно при n=0: имеем 0=0,5⋅0⋅(0+1) (посылка индукции).

Предположим, что доказываемое утверждение верно для n=k (индуктивное предположение), то есть

0+1+…+k = 0,5k(k+1).

Покажем, что тогда оно верно и для n=k+1, то есть

0+1+…+k+(k+1) = 0,5(k+1)(k+2)

(индуктивный шаг). Сумма во втором равенстве отличается от суммы из первого равенства слагаемым k+1. Поэтому, в силу индуктивного предположения, получаем

0+1+…+k+(k+1) = 0,5k(k+1)+k+1 = 0,5(k+1)(k+2),

что и требовалось доказать.

В соответствии с принципом математической индукции, доказываемое утверждение верно для всех n.

2) Число подмножеств множества, содержащего n элементов, равно 2ⁿ.

Доказательство. Утверждение верно при n=0: пустое множество ∅ (единственное множество, содержащее 0 элементов) имеет ровно одно подмножество ∅.

Предположим теперь, что всякое множество с n=k элементами имеет 2k подмножеств, и покажем, что множество с n=k+1 элементами имеет 2^k+1 подмножеств. Пусть A – произвольное множество с n=k+1 элементами. Так как k+1>0, то A не пусто и содержит хотя бы один элемент. Пусть a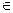A. Разобьем совокупность всех подмножеств множества A на два класса. В класс U входят все подмножества, содержащие a, в класс V входят все подмножества, не содержащие a:

U={X⊂A | a∈X}; V={Y⊂A | a∉Y}.

Положим A’=A\{a}. Множество A’ содержит k элементов, так что по индуктивному предположению, число его подмножеств равно 2^k. Но подмножества множества A’ – это в точности подмножества множества A, не содержащие a. Следовательно, |V|=2^k. Пара взаимно обратных отображений U→V, X→X\{a} и V→U, Y→Y∪{a} устанавливает между U и V взаимно однозначное соответствие, так что |U|=|V|=2^k. Поэтому общее число подмножеств множества A составляет

|U|+|V|=2^k +2^k =2^k+1,

что и требовалось доказать.

Иногда принцип полной индукции применяется в следующей форме.

Пусть P – утверждение относительно натуральных чисел n такое, что

1) P верно для n=n₀;

2) из справедливости P(n) для n= n₀, n₀+1, …, n₀+k следует справедливость P(n) для n= n₀+k+1.

Тогда P верно для всех n≥ n₀.

Принцип полной индукции в этой форме может быть сведен к предыдущей формулировке заменой утверждения P утверждением P’: утверждение P имеет место для всех t, таких, что n₀≤t≤n.

Возможны и другие модификации принципа полной индукции

Теорема. Всякое непустое подмножество натурального ряда содержит наименьший элемент.

Доказательство. Пусть A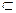N – непустое подмножество. Возможны два случая: 0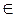A и 0∉A. В первом случае 0 является наименьшим элементом множества A. Рассмотрим второй случай. Предположим, что в A нет наименьшего элемента. Пусть A’ – это множество всех таких n, что ни одно число t из промежутка от 0 до n не содержится в A. Так как 0∉A, то 0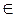A’. Далее, если kA’, то и k+1A’. В самом деле, в противном случае мы имели бы 0,1,…,k∉A, но k+1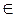A – а это означает, что k+1 – наименьший элемент множества A в противоречие с предположением об отсутствии такового. По аксиоме индукции множество A’ совпадает с N. Но это находится в противоречии с предположением о том, что множество A не пусто.

Раздел 7. ОСНОВЫ ТЕОРИИ ГРАФОВ.

Дата добавления: 2014-01-04