Тема 7.3 Метрические характеристики графа

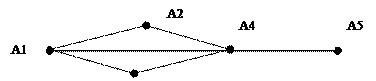Пусть дан граф:

	А3

Как от вершины А1 дойти до А5?

Существуют следующие пути:

1. <A1,A4>,<A4, A5>

2. <A1, A2>,<A2, A4>,<A4, A5>

3. <A1, A3>,<A3, A4>,<A4, A5>

4. <A1, A4>,<A4, A2>,<A2, A1>,<A1, A3>,<A3, A4>,<A4, A5>

5. <A1, A4>,<A4,A2>,<A2, A1>,<A1, A4>,<A4, A5> - не является путем, т.к. ребро <A1, A4> встречается дважды.

Путем от вершина А1 до вершины Аn называется такая последовательность ребер, ведущая от А1 до Аn, что любые два соседних ребра имеют общую вершину и ни одного ребра не встречается дважды.

Путь, в котором начальные и конечные вершины совпадают называют циклом.

Путь от вершины А1 до Аn называется простым, если он не проходит ни через одну из вершин графа более одного раза.

Цикл называется простым, если он не проходит ни через одну из вершин графа более одного раза.

Длиной пути (цикла) называется количество ребер его составляющих.

Дан граф. Найти пути от А1 до А6 и определить их длину

1. <A1,A6>, d=1

2. <A1, A2>,<A2, A6>, d=2

3. <A1, A2>,<A2, A5>,<A5, A4>,<A4, A3>,<A3, A2>,<A2, A6>, d=6

4. 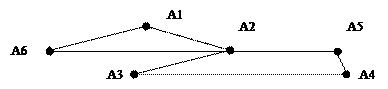<A1, A2>,<A2, A3>,<A3, A4>,<A4, A5>,<A5, A2>,<A2, A6>, d=6

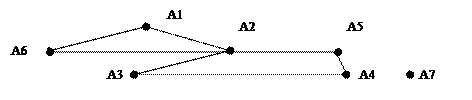Расстоянием от вершины А до вершины В называется длина наименьшего пути, если не существует пути от А до В, то считают что расстояние равно бесконечности.

S(A1,A6)=1

S(A1, A7)=∞

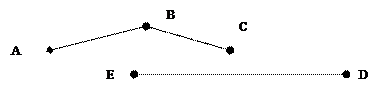Вершины А и В называются связными, если не существует пути связывающего их.

Вершины:

1. A и D – несвязные

2. A и Е – несвязные

3. А и В – связные

4. А и С – связные

Дата добавления: 2014-01-04