Лабораторная работа № 3

Полный граф, его свойства. Теорема о сумме степеней вершин графа

Цель работы:

1) Рассмотреть такую характеристику графа как вершина.

2) Изучить понятия полный граф.

3) Дать определение степени вершины.

4) Научиться определять четность вершины.

Литература:

1) "Графы и их применение", Березина Л.Ю., М: Просвещение, 1979г.

2) "Теория графов. Алгоритмический подход", Кристофидес П.

3) "Применение теории графов в программировании", Евстигнеев В.А. - М.: Наука, 1985г.

Порядок выполнения работы:

I Разработать схему алгоритмов основной программы и подпрограмм.

II Написать и отладить программу на языке Turbo Pascal.

Задание:

Граф задан матрицей смежности

М =

Для графа, заданного своей матрицей смежности, определить степени всех его вершин.

Краткие теоретические сведения:

Граф называется полным, если каждые две его вершины соединены одним и только одним ребром.

Степенью вершины называется число ребер графа, которым принадлежит эта вершина.

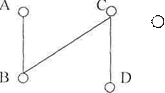Е

Степ. А=1

Степ. В=2

Степ. С=2

Степ. D=l

Стен. Е=0

Вершина называется нечетной, если её степень - число нечетное. Вершима называется четной, если её степень - число четное.

Степень каждой вершины полного графа на единицу меньше числа его вершин.

Теорема о сумме степеней графа

В графе Г - сумма степеней всех его вершин, есть число четное, равное

удвоенному числу его ребер, т.е.

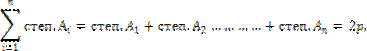
где р - число ребер графа, n- число вершин.

Содержание отчета:

1) Составление алгоритмов.

2) Написание программы на языке Turbo Pascal.

3) Отладка программы.

Контрольные вопросы:

1) Что такое полный граф?

2) Дайте понятие степени вершины графа?

3) Какая вершина графа называется четной?

4) Какая вершина графа называется нечетной?

5) Сформулируйте теорему о сумме степеней вершин графа?

Дата добавления: 2014-01-04