
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П Л А Н. 2. Скалярний добуток та його властивості
|
|
|
|
1. Лінійні дії з векторами.
2. Скалярний добуток та його властивості.
3. Довжина вектора, кут між векторами, проекції.
4. Розклад вектора за базисом.
Скалярні в еличини характеризуються своїм числовим значенням (об’єм, маса, температура…). Векторні * –крім числового значення мають ще й напрям (сила, швидкість…).
*лат. Vector (переносник) ввів у 1848 р. Гамільтон
Геометрично векторна величина зображається напрямленим відрізком:
 А
А 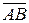 В
В
 Модуль вектора (його довжина) позначається
Модуль вектора (його довжина) позначається 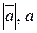 .
.

 До лінійних дій з векторами належать додавання і віднімання векторів, множення вектора на число.
До лінійних дій з векторами належать додавання і віднімання векторів, множення вектора на число.
1) Додавання. 
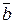
 а) правило трикутника
а) правило трикутника
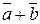
 |
б) правило паралелограма 
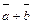

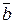

 2) Віднімання
2) Віднімання

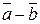

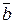
3) Множення вектора на число (скаляр)

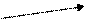

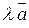
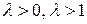
Нульовим називається вектор, початок якого збігається з кінцем (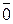 ). Напрям його невизначений, а довжина дорівнює 0.
). Напрям його невизначений, а довжина дорівнює 0.
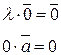
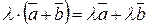
Одиничним називається вектор, довжина якого дорівнює одиниці.
Одиничний вектор, напрям якого збігається з напрямом вектора  називається ортом вектора
називається ортом вектора  і позначається
і позначається 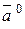
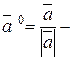 орт
орт
2.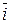 та
та 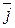 -одиничні вектори на осях х та у в координатній площині.
-одиничні вектори на осях х та у в координатній площині.

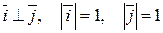
у
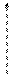

 В
В
 у
у 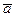



 С
С



0  х
х
 х
х
 х – проекція
х – проекція  на Ох
на Ох
 у – проекція
у – проекція  на Оу
на Оу
З 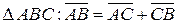

Напрям 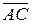 такий же, як і у орта
такий же, як і у орта 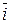 ,
, 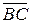 - у орта
- у орта 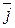 ; довжини:
; довжини:

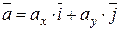
| - розклад вектора за ортонормованим Базисом на площині |
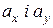 -координати вектора
-координати вектора
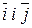 - ортонормований базис на площині.
- ортонормований базис на площині.
Записують так: 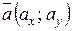
В просторі ортонормований базис утворюють вектори 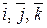
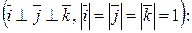
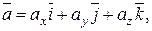

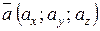
z


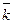



 0
0 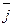 y
y
x
Якщо задано вектор 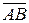 , де А (x1; y1; z1) –початок вектора, В (x2; y2; z2) – кінець, то
, де А (x1; y1; z1) –початок вектора, В (x2; y2; z2) – кінець, то 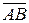 (х2-х1; у2-у1; z2-z1).
(х2-х1; у2-у1; z2-z1).
Дії з векторами в координатній формі.
1) 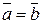 , якщо
, якщо 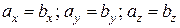
2) 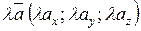
3) 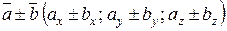
Колінеарними називають вектори, якщо вони лежать на одній прямій або на паралельних прямих.




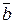
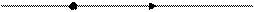
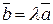 - умова колінеарності векторів, тобто якщо вектори колінеарні, то один з них можна виразити через другий.
- умова колінеарності векторів, тобто якщо вектори колінеарні, то один з них можна виразити через другий.
Якщо вектори задані в координатній формі, то відповідні координати їх пропорційні: 
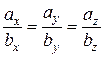
Приклад: Чи колінеарні вектори
 (-2; 1; -3) і
(-2; 1; -3) і 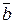 (4; -2; -3)?
(4; -2; -3)?
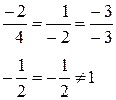
Вектори не колінеарні
Три вектори називаються компланарними, якщо вони лежать в одній площині, або в паралельних площинах.
3. Скалярним добутком двох векторів називається добуток довжин цих векторів на косинус кута між ними
^
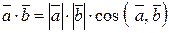 -число!
-число!
Властивості:
1) 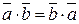
2) 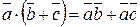
3) 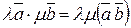
| 4) | 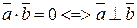
|
^
5) 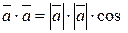 (
(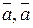 )
)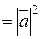 , звідки
, звідки 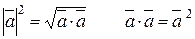
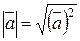
|
Скалярний добуток двох векторів, заданих координатами в прямокутній системі координат, дорівнює сумі добутків їхніх відповідних координат:
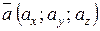
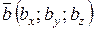
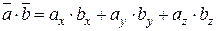
4. Довжина вектора в координатній формі:
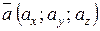
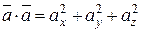
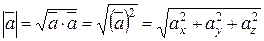
Кут між векторами:
^
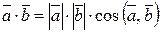
^
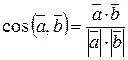
|
Напрямні косинуси вектора:
 у
у


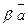


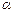 Напрямними косинусами вектора
Напрямними косинусами вектора 
називаються косинуси кутів, які
 0 х вектор утворює з осями координат
0 х вектор утворює з осями координат
Ох, Оу, Оz відповідно.
Тоді 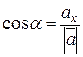
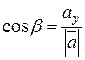
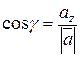
 (сума квадратів напрямних косинусів довільного вектора дорівнює 1).
(сума квадратів напрямних косинусів довільного вектора дорівнює 1).
Приклади:
1) При якому значенні у вектори будуть перпендикулярними?
 (5; -4; 8)
(5; -4; 8)
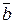 (2; у-1; 4)
(2; у-1; 4)
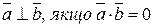
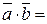 10-4 х (у-1)+32=46-4у
10-4 х (у-1)+32=46-4у
46-4у=0, у= 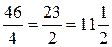
2) вектори  і
і 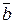 колінеарні, знайти х і z:
колінеарні, знайти х і z:
 (х; 3; -2)
(х; 3; -2)
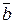 (2; 6; -z)
(2; 6; -z)
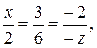
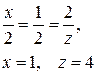
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 439; Нарушение авторских прав?; Мы поможем в написании вашей работы!