
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П Л А Н. 1. Конспект, підготовка до практичного заняття. 1. Конспект, підготовка до практичного заняття
|
|
|
|
Завдання додому
1. Конспект, підготовка до практичного заняття
2. [1] c. 32-42, 54-58
Питання для самоконтролю
1. Лінійні дії з векторами.
2. Скалярний добуток та його властивості.
3. Довжина вектора, кут між векторами, проекції.
4. Розклад вектора за базисом.
Л Е К Ц І Я 9
Тема: Векторні простори
Мета: сформувати поняття n-вимірного векторного простору; ознайомити з лінійною комбінацією векторів; лінійно залежними та незалежними стемами векторів, базисним мінором, базисом, розкладом вектора за базисом, рангом системи векторів.
Література: [1, с. 50-55]; [6, с. 109-116].
1. n-вимірні векторні простори. Лінійна комбінація векторів.
2. Лінійно залежні та лінійно незалежні комбінації векторів. Базисний мінор.
3. Базис. Розклад вектора за даним базисом.
4. Ранг системи векторів
n-вимірним вектором називається упорядкована множина n дійсних чисел, які називаються координатами вектора.
n-вимірний вектор можна записати як матрицю-рядок або матрицю-стовпець:
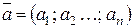 або
або 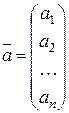
Число координат вектора називається розмірністю вектора.
Дії з n-вимірними векторами
1) Порівнюють вектори тільки однієї розмірності.
2) 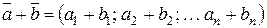
3) 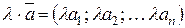
4)  або
або 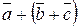
5) Існує нульовий вектор (всі координати якого дорівнюють 0): 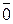 =(0; 0;... 0)
=(0; 0;... 0)
6) Існують одиничні вектори (у яких одна з координат дорівнює 1, а інші 0; довжина одиничного вектора дорівнює 1):
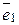 =(1; 0;...0),
=(1; 0;...0), 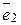 =(0; 1; 0;...0),...
=(0; 1; 0;...0),...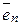 =(0; 0;...1)
=(0; 0;...1)
7) 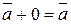
n-вимірним векторним простором називається множина всіх n-вимірних векторів, в якій операції додавання векторів та множення вектора на число визначені, як в пунктах 2 і 3.
Позначається Rn
Зауваження: Простори R1, R2, R3 є окремими випадками простору Rn. Їх можна зобразити геометрично; для n>3 простори Rn геометрично вже уявити не можна, проте вони відіграють важливу роль в науці і техніці.
|
|
|
1) У системі лінійних рівнянь з n невідомими кожне рівняння можна розглядати як (n+1) – вимірний вектор; наприклад перше рівняння:  .
.
2) Розв’язок системи рівнянь з n невідомими є n -вимірним вектором.
3) Кожний рядок матриці Аmn є n-вимірним вектором, а кожний стовпець m-вимірним. Рядки називаються горизонтальними, а стовпці – вертикальними векторами матриці.
Система n-вимірних векторів
Нехай дана система n-вимірних векторів: 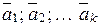 , і дані скаляри (числа):
, і дані скаляри (числа): 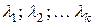 . Нехай
. Нехай
* 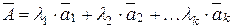 - лінійна комбінація векторів, а числа
- лінійна комбінація векторів, а числа 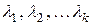 - лінійна комбінація векторів, а числа
- лінійна комбінація векторів, а числа 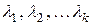 - коефіцієнти лінійної комбінації.
- коефіцієнти лінійної комбінації.
Вираз * визначає розклад вектора  за векторами
за векторами 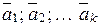 .
.
2. Розглянемо систему з k n-вимірних векторів: 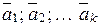 .
.
Вектори називаються лінійно залежними, якщо хоча б один з них можна лінійно виразити через інші.
Або: якщо лінійна комбінація системи векторів  рівна нулю за умови, що хоча б один із коефіцієнтів
рівна нулю за умови, що хоча б один із коефіцієнтів  не дорівнює нулю, то вектори називаються лінійно залежними.
не дорівнює нулю, то вектори називаються лінійно залежними.
Вектори називаються лінійно незалежними, якщо ні один із векторів не можна лінійно виразити через інші.
Або: Вектори називаються лінійно незалежними, якщо їх лінійна комбінація дорівнює нулю тільки за умови, що всі 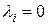
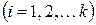 .
.
Приклад: Чи будуть вектори лінійно залежними: 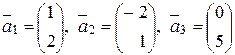 ?
?
Складемо лінійну комбінацію цих векторів і знайдемо, при яких значеннях 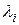 лінійна комбінація дорівнює 0.
лінійна комбінація дорівнює 0.

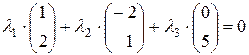
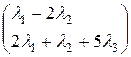 - в правій частині одержаної рівності нульовий вектор, значить його координати повинні дорівнювати 0.
- в правій частині одержаної рівності нульовий вектор, значить його координати повинні дорівнювати 0.
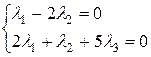

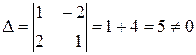
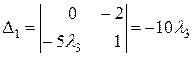

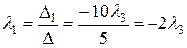
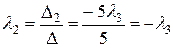

Система має нескінченну множину розв’язків за умови 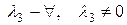 , значить дані вектори лінійно залежні.
, значить дані вектори лінійно залежні.
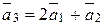
3. Нехай дана система n-вимірних векторів: 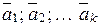
Рангом системи n-вимірних векторів називається число, яке дорівнює найбільшому числу лінійно незалежних векторів.
Базисом системи векторів називається впорядкована сукупність найбільшого числа лінійно незалежних векторів цієї системи.
|
|
|
Значить, ранг системи векторів дорівнює числу векторів, які утворюють базис.
В одній і ті й же системі векторів може бути декілька базисів, але кількість базисних векторів в кожному базисі одна й та ж.
Щоб знайти базис системи векторів записують матрицю з координат цих векторів, записаних у вигляді матриці-стовпця. Знаходять ранг матриці, який буде дорівнювати рангу системи векторів, а базисними векторами будуть вектори, які відповідають базисним стовпцям матриці.
Базисом n-вимірного векторного простору Rn називається довільна впорядкована система з n лінійно незалежних векторів.
Якщо система векторів 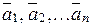 є базисом n-вимірного векторного простору Rn, то довільний вектор цього простору можна подати у вигляді лінійної комбінації базисних векторів:
є базисом n-вимірного векторного простору Rn, то довільний вектор цього простору можна подати у вигляді лінійної комбінації базисних векторів:
** 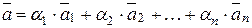 , де
, де 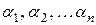 - координати
- координати  в базисі
в базисі 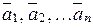
Вираз ** називається розкладом вектора  за даним базисом.
за даним базисом.
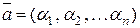
Система n-вимірних векторів в Rn, яка складається більше, ніж з n векторів, завжди лінійно залежна!
В двомірному просторі базис має 2 вектори (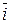 та
та 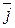 ), а система більше 2-х векторів завжди лінійно залежна.
), а система більше 2-х векторів завжди лінійно залежна.
Система більш, ніж 3-х векторів, в тривимірному просторі також лінійно залежна.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 325; Нарушение авторских прав?; Мы поможем в написании вашей работы!