
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П Л А Н. 1. Конспект; підготовка до практичного заняття
|
|
|
|
Завдання додому.
1. Конспект; підготовка до практичного заняття.
2. [2] с. 70-76
Питання для самоконтролю
1. n-вимірні векторні простори.
2. Лінійна комбінація векторів.
3. Лінійно залежні та лінійно незалежні комбінації векторів.
4. Базисний мінор.
5. Базис.
6. Розклад вектора за даним базисом.
7. Ранг системи векторів
Л Е К Ц І Я 10
Тема: Пряма лінія на площині
Мета: ознайомити з різними видами рівнянь прямої на площині, кутом між двома прямими, відстанню від точки до прямої
Література: [1, с. 75-83]; [6, с. 131-142].
1. Різні види рівнянь прямої на площині.
2. Кут між двома прямими.
3. Відстань від точки до прямої.
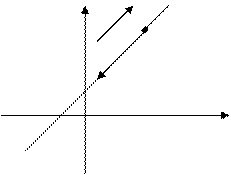 1. Точка на площині характеризується двома координатами: абсцисою та ординатою (М (х; у)). Рівняння прямої містять координати х та у у першому степені.
1. Точка на площині характеризується двома координатами: абсцисою та ординатою (М (х; у)). Рівняння прямої містять координати х та у у першому степені.
1) у  Нехай дана пряма на площині.
Нехай дана пряма на площині.
М1 М1 (х1; у1) – фіксована точка прямої.
М (х; у) – довільна точка прямої (змінна)
М
0 х
Вектор  = (m; n) паралельний прямій.
= (m; n) паралельний прямій.
Потрібно за цими даними скласти рівняння прямої.
Вектори  і
і  колінеарні, значить їх координати пропорційні.
колінеарні, значить їх координати пропорційні.
 = (х-х1; у-у1)
= (х-х1; у-у1)
Умова колінеарності:

| Канонічне рівняння прямої на площині |
2) Перетворимо одержане рівняння прямої:
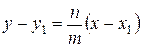
Відношення 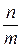 називають кутовим коефіцієнтом прямої
називають кутовим коефіцієнтом прямої 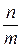 =k
=k

| Рівняння прямої, яка проходить через т. М в |

| напрямі (напрям вказує k) |
у

 М1
М1



0 х
 |
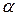 - кут нахилу прямої до осі абсцис
- кут нахилу прямої до осі абсцис

k>0 – кут гострий, k<0 – тупий
3) Перетворимо одержане рівняння:
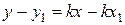

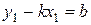
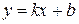
| Рівняння прямої з кутовим коефіцієнтом |
 – ордината точки, в якій пряма перетинає вісь Оу
– ордината точки, в якій пряма перетинає вісь Оу
 |
 у
у




0 х
4) Рівняння прямої, яка проходить через дві задані точки.

 у
у
 М2 М1 (х1; у1)
М2 М1 (х1; у1)
 М1 М2 (х2; у2)
М1 М2 (х2; у2)
 |
0 х Запишемо рівняння прямої:
у-у1=к (х-х1)
у2-у1=к (х2-х1)
Так як М2 (х2; у2) лежить на прямій, то її координати задовольняють рівнянню прямої, тому замість х і у можна підставити координати т. М2.
Розділимо обидві частини рівнянь і одержимо:

| Рівняння прямої, яка проходить через дві задані точки |
5) Загальне рівняння прямої
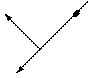 |
 М1
М1


М
 =(А; В)
=(А; В)  прямій
прямій

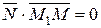


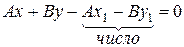
позначимо С

| Загальне рівняння прямої, де А і В – координати |
| нормального вектора прямої, С – вільний член |
Дослідження загального рівняння прямої
а) Нехай А=0, Ву+С=0 – пряма, паралельна осі Ох
 |
у





0 х
б) Нехай В=0, Ах+С=0 – пряма, паралельна осі Оу

 у
у


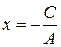
0 х

в) С=0, Ах+Ву=0 – пряма, проходить через початок координат
 |
 у
у

 0 х
0 х
6) Рівняння прямої у відрізках на осях.




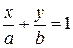
| Рівняння прямої у відрізках на осях |

 у
у  і
і  - відрізки, які
- відрізки, які
 віднімає пряма на осях Ох та Оу
віднімає пряма на осях Ох та Оу


 0
0  х
х
2. Нехай дані рівняння двох прямих: 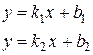

 у
у
 |
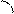
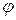


0 х
Якщо рівняння прямих задані в загальному вигляді Ах+Ву+С=0, то
| Кутовий коефіцієнт | 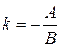
|
Умова паралельності прямих
 |
 у
у


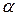 1
1 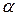 2
2
 0 х
0 х
 , значить
, значить


|
Умова перпендикулярності прямих
 1
1
 |
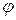 900
900
 2
2

 (не існує)
(не існує)


|
3.
 М0 (х0; у0) Нехай пряма задана рівнянням
М0 (х0; у0) Нехай пряма задана рівнянням
 Ах+Ву+С=0
Ах+Ву+С=0
 |
М0 (х0; у0) – точка, яка не лежить на цій прямій.
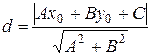
Приклади:
1) Записати рівняння прямої, яка проходить через точку М (-1; 2) перпендикулярно прямій 2х-у+1=0



2) Загальне рівняння прямої записати у відрізках на осях і побудувати пряму:

 y
y



 2
2







 -5 0 x
-5 0 x

3) Записати рівняння прямої, яка проходить через точки М1 (-2; 5), М2 (3; 5)



 - пряма, паралельна осі Ох
- пряма, паралельна осі Ох
Додатково: Побудова система нерівностей.
Довільна пряма ділить площину на дві півплощини Ах+Ву+С=0
 у Ах+Ву+С
у Ах+Ву+С або Ах+Ву+С
або Ах+Ву+С 0 – ці нерівності,
0 – ці нерівності,
 описують множину точок, які належать
описують множину точок, які належать
одній із півплощин
 |
0 х
Для того, щоб побудувати шукану півплощину, потрібно:
1) побудувати пряму Ах+Ву+С=0;
2) з довільної півплощини вибрати точку з відомими координатами і ці координати підставити в нерівність. Якщо зміст нерівності зберігся, то нерівність описує ту півплощину, з якої була вибрана точка. Якщо зміст нерівності не зберігся, то нерівність описує другу півплощину.

у
 | |||
 | |||

 3
3





 2
2
 -2
-2















 0 10 х
0 10 х
 |  | ||
-5
 |
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 338; Нарушение авторских прав?; Мы поможем в написании вашей работы!