
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ймовірність багатокрокового переходу системи. Вектор початкового стану системи
|
|
|
|
Імовірність переходу системи зі стану  за
за  кроків у стан
кроків у стан  називається N-кроковою матрицею ймовірності переходів.
називається N-кроковою матрицею ймовірності переходів.
Нехай задана матриця однокрокового переходу π і необхідно обчислити елементи матриці  . При
. При 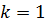 елементі матриці:
елементі матриці:

Як визначити елементи матриці при двукроковому переході, коли  .
.
Двокроковий перехід зображений на малюнку:

Існує  можливих шляхів переходу системи зі стану
можливих шляхів переходу системи зі стану  в стан
в стан 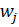 за 2 кроки.
за 2 кроки.
Імовірність випадкового процесу для кожного шляху переходу системи обчислюється за формулами множення ймовірностей незалежних випадкових величин.
Тобто 2-крокова ймовірність переходу зі стану  в
в 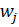 :
:

Аналогічно на  -тому кроці
-тому кроці  :
:

Перший стан, з якого система починає свій перехід може бути заданим або визначеним.
У загальному випадку для системи задається вектор початкового стану:
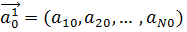
- ймовірність того, що система знаходиться в стані  . При цьому ймовірність
. При цьому ймовірність  .
.
Приклад. Необхідно дослідити яким видом транспорту: тролейбусом, автобусом чи метро користується середньостатистичний мешканець міста, добираючись до роботи, якщо відомо, що коли він в певний день протягом тижня добирався автобусом, то ймовірність того, що наступного дня він добирається автобусом - 0,6, тролейбусом - 0,35, метро - 0,05. Якщо він добирався тролейбусом, то ймовірність того, що він на наступний день буде добиратися тролейбусом - 0,7, автобусом - 0,25, метро - 0,05. Якщо він добирався на метро, то ймовірність того, що він на наступний день буде добиратися на метро - 0,8, автобусом - 0,005, тролейбусом - 0,15.
Побудувати матрицю однокрокового переходу випадкового процесу, який може відповідати трьом видам громадського транспорту і визначити ймовірність того, що житель буде користуватися автобусом в середу або п'ятницю, якщо в понеділок він їхав на метро.
Рішення:
Позначимо через:
 - використання автобуса;
- використання автобуса;
 - використання троллейбуса;
- використання троллейбуса;
 - використання метро.
- використання метро.
Матриця однокрокового переходу системи має наступний вигляд:
a=(0;0;1)


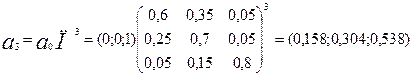
Відповідь: ймовірність того, що в середу житель вибере автобус дорівнює 0,158.
Автобус у Пт  , ймовірність того що житель вибере автобус в Пт дорівнює
, ймовірність того що житель вибере автобус в Пт дорівнює 
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 772; Нарушение авторских прав?; Мы поможем в написании вашей работы!