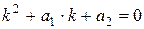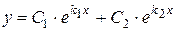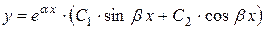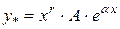П Л А Н. 1. Диференціальні рівняння з відокремлюваними змінними

Завдання додому.

1) Конспект; [1] с. 421 - 451;

[2] с. 325 – 339.

Питання для самоконтролю

1. Диференціальні рівняння з відокремлюваними змінними.

2. Лінійні диференціальні рівняння першого порядку.

Л Е К Ц І Я 29

Тема: Лінійні диференціальні рівняння із сталими коефіцієнтами

Мета: сформувати поняття лінійного диференціального рівняння другого порядку; ознайомити з однорідними та неоднорідними рівняннями.

Література: [1, с. 470-482]; [6, с. 449-459].

1. Лінійні диференціальні рівняння другого порядку.

2. Однорідні та неоднорідні рівняння.

1. Розглянемо диференціальні рівняння другого порядку:

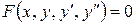- запис рівняння в неявному вигляді;

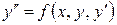- нормальний (або явний) запис диференціального рівняння другого порядку.

Розв’язком рівняння на деякому інтервалі (a; b) називається неперервна функція 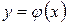на цьому інтервалі, для якої існують похідні 1-го та 2-го порядку, така, що при підстановці в дане рівняння перетворює його в тотожність.

Графік розв’язку диференціального рівняння називається його інтегральною кривою.

Для диференціальних рівнянь вищих порядків, як і для рівнянь першого порядку, розглядається задача Коші або задача з початковими умовами.

Для рівнянь другого порядку ця задача ставиться так: серед усіх розв’язків рівняння знайти такий розв’язок 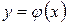, , 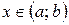який при задовольняє умови:

,

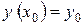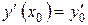
Розглянемо види диференціальних рівнянь другого порядку:

а) Неповні (містять тільки 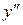і функцію, яка залежить від х): .

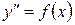Щоб знайти загальний розв’язок такого рівняння, потрібно праву частину проінтегрувати два рази.

Приклад: Знайти загальний розв’язок рівняння .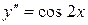

,

.

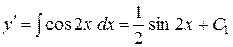Відповідь: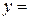

2. б) Лінійні диференціальні рівняння із сталими коефіцієнтами – це рівняння виду

, де 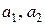- дійсні числа.

Якщо 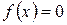, то рівняння називається лінійним однорідним диференціальним рівнянням другого порядку із сталими коефіцієнтами (ЛОДР).

Якщо 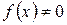, то таке рівняння називається неоднорідним (ЛНДР).

Розглянемо спочатку розв’язки лінійного однорідного диференціального рівняння другого порядку із сталими коефіцієнтами

Теорема (про структуру загального розв’язку ЛОДР)

Якщо функції та 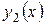є розв’язками рівняння (*), то функція також буде розв’язком ЛОДР при умові, що та 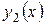- лінійно незалежні, тобто .

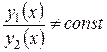- загальний розв’язок ЛОДР.

Ейлер запропонував шукати частинні розв’язки цього рівняння у вигляді , де k – стала (дійсна чи комплексна), яку треба знайти.

,

,

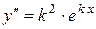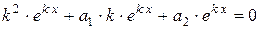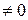, тоді - характеристичне рівняння

лінійного однорідного диференціального рівняння другого порядку.

Позначимо корені характеристичного рівняння через k₁ і k₂.

Формули для загального розв’язку ЛОДР

1) Якщо k₁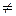k₂ (дійсні, різні числа) (дискримінант D>0), то

2) Якщо k₁=k₂ (дійсні, рівні числа)

(D=0), то

3) Якщо k_{1, 2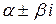} = (комплексно - спряжені числа) (D<0), то

Приклади: Знайти загальний розв’язок:

1)

складаємо характеристичне рівняння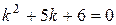

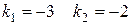
2)

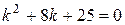
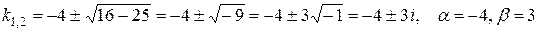
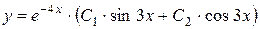
Розглянемо розв’язки лінійного неоднорідного диференціального рівняння другого порядку із сталими коефіцієнтами

.

Теорема (про структуру загального розв’язку ЛНДР)

Загальний розв’язок ЛНДР являє собою суму загального розв’язку відповідного однорідного рівняння і довільного частинного розв’язку даного рівняння.

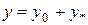, де у₀ – загальний розв’язок відповідного ЛОДР,

у_* - частинний розв’язок ЛНДР.

Є рівняння із спеціальною правою частиною, для яких знайдені частинні розв’язки.

1) 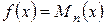, де - многочлен (поліном) степеня n.

, де

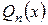- многочлен (поліном) степеня n з невідомими коефіцієнтами;

r знаходимо з умови:

1. r=0, якщо 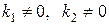(k₁ і k₂ – корені характеристичного рівняння).

2. r=1, якщо k₁ =0 (або k₂ =0).

Приклад: Знайти загальний розв’язок рівняння: .

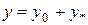
у₀ -?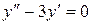

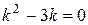
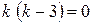
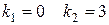
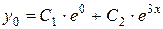
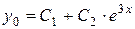
у_* -?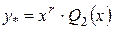

=

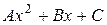
так як k₁ = 0, то r = 1

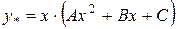
Потрібно знайти А, В, С:

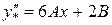
Підставимо в дане рівняння:

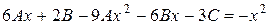
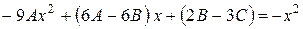
Застосуємо метод невизначених коефіцієнтів:

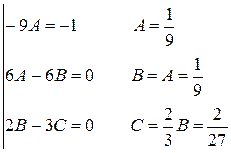
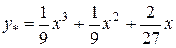
- загальний розв’язок рівняння.

2) , де М і 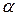- сталі числа.

, де А – невідоме число;

r знаходимо з умови:

1. r = 0, якщо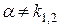

2. r = 1, якщо (або )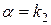

3. r = 2, якщо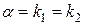

Приклад: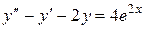

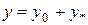
у₀ -?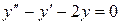

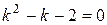
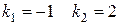
у_* -?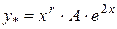

так як , то r = 1

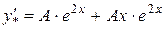
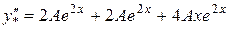
Підставимо в дане рівняння:

,

,

,

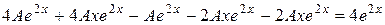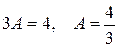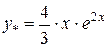
- загальний розв’язок

3) 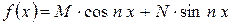, де M і N – сталі числа.

, де А і В – невідомі числа;

r знаходимо з умови:

1. r = 0, якщо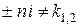

2. r = 1, якщо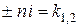

Приклад: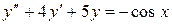

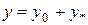
у₀ -?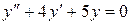

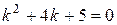
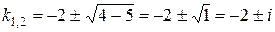
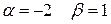
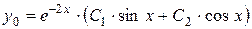
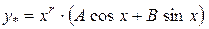
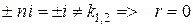
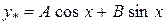
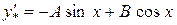
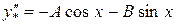
Підставимо в дане рівняння:

;

;

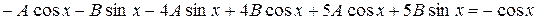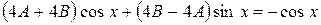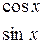
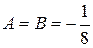
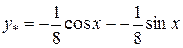
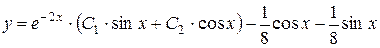- загальний розв’язок

Дата добавления: 2014-01-04