
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П Л А Н. 1. Однорідні лінійні різницеві рівняння
|
|
|
|
Завдання додому
Конспект; [4] с. 66 – 71
Питання для самоконтролю
1. Однорідні лінійні різницеві рівняння.
2. Неоднорідні лінійні різницеві рівняння.
Л Е К Ц І Я 31
Тема: Числові ряди. Основні поняття.
Мета: сформувати поняття числового ряду; ознайомити із збіжними і розбіжними рядами, властивостями збіжних рядів, необхідною умовою збіжності ряду
Література: [1, с. 493-497]; [6, с. 464-473].
1. Ряди. Основні значення.
2. Збіжність рядів, властивості збіжних рядів.
3. Необхідна умова збіжності
1. Нехай задано послідовність дійсних чисел u1, u2, u3, …un,…
Рядом називається вираз u1+ u2+ … +un +…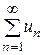 , де u1, u2, u3 - члени ряду,
, де u1, u2, u3 - члени ряду,
un – загальний член ряду.
Ряд вважається заданим, якщо його загальний член un заданий формулою,
Приклад 1: 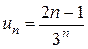
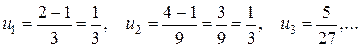
Запишемо ряд: 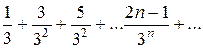
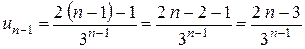
Приклад 2: Записати формулу загального члена ряду
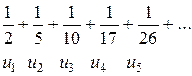
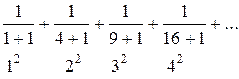
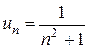
2. Нехай задано числовий ряд
u1+ u2+ u3 +… + un +…
Складемо частинні суми ряду:
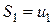
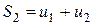
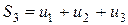
...
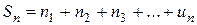
...
Одержимо послідовність частинних сум
Якщо існує границя послідовності частинних сум ряду (дорівнює якомусь значенню S), то такий ряд називається збіжним:
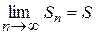 - ряд збіжний,
- ряд збіжний,
S – сума ряду.
Якщо границя послідовності частинних сум ряду не існує, то ряд називається розбіжним.
Властивості збіжних рядів
1) Якщо 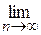 Sn = S, то S – сума ряду.
Sn = S, то S – сума ряду.
2) Якщо ряд u1+ u2+ u3 +… + un +… збіжний, то збіжний і ряд
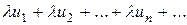 , де
, де 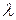 - число, причому сума такого ряду дорівнює
- число, причому сума такого ряду дорівнює 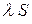
3) Нехай два ряди u1+ u2+ … + un +…
v1+ v2+ … + vn +… збіжні, тоді збіжний і ряд 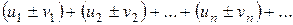 , а сума його дорівнює
, а сума його дорівнює 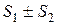 .
.
Зауваження: скорочений запис ряду
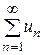 = u1+ u2+ … + un +…
= u1+ u2+ … + un +…
Приклад: Знайти суму ряду
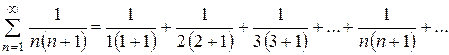
Знайдемо частинну суму Sn:
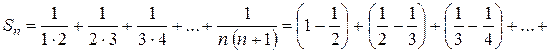
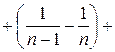
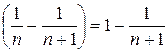
Знайдемо суму ряду:
 S=
S=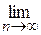 Sn =
Sn =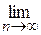
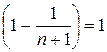
 |
3. Необхідна умова збіжності ряду:
Якщо ряд 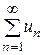 збіжний, то
збіжний, то 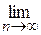
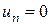
Достатня умова розбіжності ряду:
Якщо 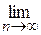
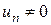 , то ряд
, то ряд 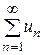 розбіжний.
розбіжний.
Приклад: Використовуючи необхідну умову збіжності, перевірити поведінку рядів:
1) 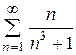 2)
2) 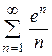 3)
3) 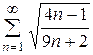
 0
0


 1)
1) 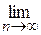
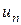 =
=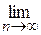
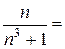
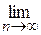
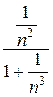 =0,
=0,
отже ряд може бути збіжним або розбіжним.
2) 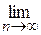
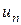 =
=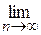
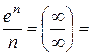
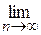
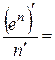
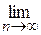
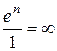 - ряд розбіжний
- ряд розбіжний
3) 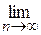
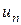 =
=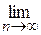
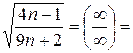
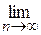
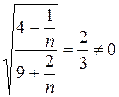 - ряд розбіжний
- ряд розбіжний
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 318; Нарушение авторских прав?; Мы поможем в написании вашей работы!