Рахунки накопичення

П Л А Н

1. Рахунки накопичення

2. Розрахунки ренти

3. Погашення боргу

Основні проблеми математики фінансів — обчислення про­стих та складних відсотків прибутку, розглянуто у розділах 3.2 та 3.3. Зараз ознайомимось з деякими іншими важливими зада­чами фінансової сфери.

Найпростішим типовим рахунком накопичення є такий раху­нок фізичної або юридичної особи, на який регулярно начисляється і зараховується (наприклад, в кінці кожного місяця або на початку

наступного року) фіксований доход та робиться ба­ланс вкладень і запланованих відсотків з врахуванням терміну одержаних вкладень.

Приклад 1. Кожного місяця робітник вносить 100 гривень на свій рахунок накопичення з одержанням прибутку величиною 1/2% за кожен місяць. Обчислити величину його накопичень: а) - безпосередньо після здійснення 25 внеску; б) безпосередньо після здійснення n внеску.

Розв'язування. а) Кожен внесок за місяць зростає в 1,005 рази (0,5% за місяць). Тому перший внесок за 24 місяця перебування ра­хунку прийме значення 100 • (1,005)²⁴. Другий внесок знаходився на рахунку 23 місяця, тому він прийме значення 100 • (1,005)²², третій вне­сок стане 100 ● (1,005)²², і т.д. Отже, загальна сума накопиченого рахун­ку робітника прийме значення

S = 100 • (1,005)²⁴ + 100(1,005)²³ +... + 100 • (1,005) + 100.

Якщо розглядати праву частину в оберненому порядку, тоді її мож­на розглядати як геометричну прогресію з першим членом b1=100 і знаменником q= 1,005. Тому, використовуючи формулу суми скінченної геометричної прогресії, одержимо

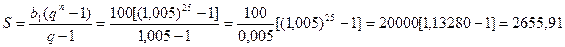
Таким чином, після 24 місяців робітник буде мати на своєму рахун­ку накопичення 2 655,9 гривень.

б) Для знаходження величини рахунку

накопичення безпосередньо після здійснення n внеску, слід рахувати (n-1) місяць першого вкладу. Після (n-1) місяця перший вклад величиною 100 гривень зросте до 100- (1,005)^n-1, другий вклад зросте до 100- (1,005)^n-2 і т.д. Таким чи­ном, загальним значенням рахунку накопичення буде сума

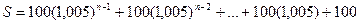
Знову одержали суму геометричної прогресії з першим членом 100 (розглядаємо її в оберненому порядку) і знаменником q= 1,005. Тому вона буде мати вигляд

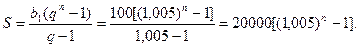(1)

Зауваження. Формула (1) дозволяє знайти величину накопичених коштів при умовах задачі за довільну кількість місяців. Наприклад, після 59 місяців на рахунку буде

20000[(1,005)⁵⁹-1] = 20000[1,34885-1]=6977 гривень

Тепер узагальнимо проведені при розв'язанні прикладу 1 міркуван­ня на випадок, коли перший внесок на рахунок накопичення дорівнює величині Р, а постійний відсоток зростання величини коштів дорівнює К за кожен певний період. У фінансових розрахунках засто­совують позначення

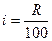(2)

При таких позначеннях величина накопичених коштів на рахунку після (n - 1) періоду їх зберігання

буде

S=P(1+i)^n-1+P(1+i)^n-2+…+P(1+i)+P

Якщо цю суму записати в оберненому порядку, то одержимо суму геометричної прогресії п членів, з першим членом b₂ = Р та знаменником q = 1 + і. Тому, згідно з формулою суми скінченної геометричної прогресії маємо

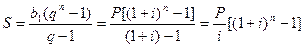(3)

Зауваження. 1) Якщо у формулі (3) покласти Р= 100, i=0,005, то ми одержимо результат прикладу 1.

2) У фінансових розрахунках формула (3) використовується у ви­гляді

S=P*s_n/i (4)

де значення s_n/i для різних n та і вказані в спеціальних розрахункових таблицях (дивись, наприклад, таблицю 1).

Так, розв'язок прикладу 1. а) за формулою (4) буде згідно таблично­му значенню s_n/i:

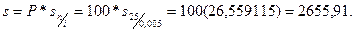
Дата добавления: 2014-01-04