
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дедуктивного рассуждения)
|
|
|
|
Правила образования языка в алфавите (синтаксис языка).
Для описания правил введем понятие метасимвол. Метасимвол – это не принадлежащее языку обозначение, которое позволяет вводить понятия и свойства этого языка, а также указать порядок, в котором должны применяться правила языка.
Введем 4 метасимвола для иллюстрации заданных правил примерами:
1) x 2) y 3) (4)). Метасимволы x и y будут служить для обозначения формул, а скобки (и) – для указания порядка применения правил.
Правила образования языка в алфавите следующие:
Базисное правило: всякое высказывание есть формул а.
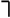 Правило индукционного шага: если x и y – формулы, то
Правило индукционного шага: если x и y – формулы, то 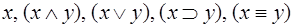 - тоже формулы.
- тоже формулы.
Правило ограничения: формулы могут образовываться только по правилам 1 и 2.
Других правил нет.
Как же метасимволы скобок указывают на порядок применения правил? Рассмотрим пример.
 Пусть, х (p/\(q\/r)). При построении формулы х правило индукционного шага применялось дважды: первый раз – при построении формулы (q\/r) из формулы q и r, а второй – при построении заключительной формулы из формул p и (q\/r). Указанные правила образования языка в алфавите используются для представления составных сколь угодно сложных высказываний.
Пусть, х (p/\(q\/r)). При построении формулы х правило индукционного шага применялось дважды: первый раз – при построении формулы (q\/r) из формулы q и r, а второй – при построении заключительной формулы из формул p и (q\/r). Указанные правила образования языка в алфавите используются для представления составных сколь угодно сложных высказываний.
Формулы языка делятся на атомы или атомарные формулы и формулы (без эпитетов), к которым относятся все составные формулы, т.е. формулы, образованные с помощью связок, а атомы – это неделимые (исходные) высказывания.
3.2.3. Правила присвоения истинностных значений формулам
(семантика языка)
По определению атом может иметь только два значения: либо ‘‘истина‘‘ (И) либо ‘‘ложь‘‘ (Л). Каждое из этих значений называют истинностным. Правила присвоения истинностных значений формулам 5-ти связок представлены в табл. 3.2.
Таблица 3.2
 x x
| y | x | x Ù y | x Ú y | x É y | x º y |
| И | И | Л | И | И | И | И |
| И | Л | Л | Л | И | Л | Л |
| Л | И | И | Л | И | И | Л |
| Л | Л | И | Л | Л | И | И |
Введем ряд новых понятий, которые понадобятся при рассмотрении следующих аспектов исчисления высказываний.
1) «Интерпретировать формулу» - приписать ей одно из двух значений истинности И или Л.
2) «интерпретация для формулы» - это набор истинностных значений всех атомов, входящих в формулу, предназначенный для одновременной замены ими самих атомов в этой формуле. Формула, содержащая К различных высказываний, допускает 2к интерпретаций.
Проиллюстрируем эти два понятия на примерах интерпретации некоторых формул (табл. 3.3):
Таблица 3.3
 x y z x y z
| y É z | x É(yÉz) | x Ù y | (x Ù y)Éz | w | w |
| И И И | Л | И | И | И | И | Л |
| И И Л | Л | Л | И | Л | И | Л |
| И Л И | И | И | Л | И | И | Л |
| И Л Л | И | И | Л | И | И | Л |
| Л И И | И | И | Л | И | И | Л |
| Л И Л | Л | И | Л | И | И | Л |
| Л Л И | И | И | Л | И | И | Л |
| Л Л Л | И | И | Л | И | И | Л |
Первые три столбца каждой строки являются одной из возможных интерпретаций.
3) семантика языка -это полный набор правил интерпретации формул. Это вся таблица 3.2.
4) «Общезначимость формулы» -это истинность формулы при всех возможных её интерпретациях. (w в табл. 3.3)
5) 
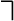 «противоречивость формулы» (невыполнимость) - это ложность формулы при всех возможных её интерпретациях (w в табл.3.3)
«противоречивость формулы» (невыполнимость) - это ложность формулы при всех возможных её интерпретациях (w в табл.3.3)
6) «эквивалентность формул» - формулы x и y эквивалентны, когда истинностные значения x и y совпадают при каждой общей интерпретации для x и.
7) «Литера» -это атом или его отрицание.
8) «дизъюнкция формул» - это формула X, образованная из исходных формул F1,F2,...,Fn с помощью дизъюнктивной (и только) связки:
X = F1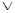 F2
F2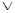 ,...
,...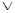 Fn.
Fn.
9) «Конъюнкция формул» -это формула Y, образованная из исходных формул F1,F2,...,Fn с помощью конъюнктивной (и только) связки:
Y = F1 F2
F2 ,...
,...  Fn.
Fn.
10) «Дизъюнкт» - это формула Z, образованная из исходных литер (и только литер) с помощью дизъюнктивной (и только) связки:
Z = A1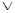 A2
A2 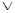 A3
A3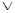 ,...
,...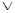 An.
An.
Эквивалентом дизъюнкта является множество входящих в него литер:

 Z = A1
Z = A1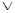 A2
A2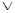 ,...
,...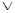 Am
Am 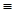 {A1 , A2 ,..., Am}
{A1 , A2 ,..., Am}
11) «R - литерный дизъюнкт» - это дизъюнкт, в котором R литер.
12) «Единичный дизъюнкт» - это дизъюнкт с одной литерой.
13) «Пустой дизъюнкт» - это дизъюнкт, в котором нет литер. Т.к. он не содержит литер, которые могли бы быть истинными при некоторой интерпретации, он всегда ложен
14)  «Область действия логических связок» - при бесскобочной записи эта область упорядочена по убыванию и соответствует последовательности º, É, Ù, Ú,.
«Область действия логических связок» - при бесскобочной записи эта область упорядочена по убыванию и соответствует последовательности º, É, Ù, Ú,.
15) Дизъюнктивная нормальная форма» - это формула
F= F1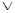 F2
F2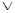 ,...
,...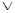 Fn, где Fi - конъюнкция литер.
Fn, где Fi - конъюнкция литер.
16) Конъюнктивная нормальная форма» -
F=F1 F2
F2 ,...
,...  Fn , где Fi - дизъюнкция литер.
Fn , где Fi - дизъюнкция литер.
17) «Выполнимая формула» - формула выполнима тогда и только тогда, когда существует, по крайней мере, одна интерпретация, при которой эта формула истинна. Эта интерпретация называется моделью формулы.
18)  «Контрарная пара формул» - это множество { A, A}
«Контрарная пара формул» - это множество { A, A}
19) «Тавтология» - общезначимая формула, истинная во всех её интерпретациях. Дизъюнкт, содержащий контрарную пару, является тавтологией.
20) «Приведенная КНФ» - это КНФ, из которой удалены тавтологии и повторения литер в пределах одного итого же дизъюнкта. Вернуться
3.2.4. Правила вывода в исчислении высказываний (стереотипы
Стереотипы выработаны за многие десятки лет, а некоторые за многие сотни лет и позволяют осуществлять корректные, т.е. без нарушения отношения логического следования, переходы от одних теорем к другим с целью приведения структуры рассуждения к канонической форме (к приведенной КНФ). Сущность канонической формы будет раскрыта в 3.2.2.6, а сейчас, до обсуждения правил вывода, введем ряд новых понятий, без которых это обсуждение невозможно.
Понятие «отношение логического следования».
Формула G является логическим следствием формул F1,F2,...,Fn тогда и только тогда, когда для каждой интерпретации I, в которой (F1 F2
F2 ,...
,...  Fn.)- истина, G также истина. F1,F2,...,Fn называются посылками, а G - заключением в отношении логического следования.
Fn.)- истина, G также истина. F1,F2,...,Fn называются посылками, а G - заключением в отношении логического следования.
Понятие «необходимые и достаточные условия логического следования».
 Формула G тогда и только тогда является логическим следствием F1,F2,...,Fn, когда формула ((F1
Формула G тогда и только тогда является логическим следствием F1,F2,...,Fn, когда формула ((F1 F2
F2 ,...
,...  Fn.)
Fn.) G) - общезначима или, когда формула (F1
G) - общезначима или, когда формула (F1 F2
F2 ,...
,...  Fn Ù G) -противоречива.
Fn Ù G) -противоречива.
Понятие «теорема в дедуктивном рассуждении.
Если формула G является логическим следствием формул F1,F2,...,Fn, то формула ((F1 F2
F2 ,...
,...  Fn)
Fn)  G) называется теоремой, а G называется заключением теоремы.
G) называется теоремой, а G называется заключением теоремы.
Понятие «доказательство в дедуктивном рассуждении» (т.е. в исчислении).
Доказательство - это аргументированное обоснование того, каким образом заключение в теореме логически следует из её посылок. Представляется доказательство в виде упорядоченной последовательности (следа) умозаключений, в результате которых устанавливается истинностное значение заключения.
Теперь о правилах вывода в исчислениях высказываний.
 Для обозначения отношения логического следования введем новый метасимвол (горизонтальная черта). Будем использовать этот метасимвол для разделения теорем – посылок и теорем – заключений. Над чертой будем записывать список теорем-посылок, под чертой - теорему-заключение. Указанная форма записи теорем будет свидетельствовать о том, что теорема – заключение является логическим следствием теорем – посылок.
Для обозначения отношения логического следования введем новый метасимвол (горизонтальная черта). Будем использовать этот метасимвол для разделения теорем – посылок и теорем – заключений. Над чертой будем записывать список теорем-посылок, под чертой - теорему-заключение. Указанная форма записи теорем будет свидетельствовать о том, что теорема – заключение является логическим следствием теорем – посылок.
Метасимвол; (точку с запятой) будем использовать в качестве разделителя в списке теорем.
Метасимвол, (запятую) будем использовать в качестве разделителя посылок внутри теоремы, имитирующего конъюнктивную связку.
 Метасимвол (прямоугольник) будем использовать для обозначения противоречивых формул.
Метасимвол (прямоугольник) будем использовать для обозначения противоречивых формул.
Рассмотрим следующий пример использования отношения логического следования:
Если барометр падает, то будет дурная погода;
Барометр падает
 Будет дурная погода
Будет дурная погода
 Перечень правил вывода следующий:
Перечень правил вывода следующий:
 1)
1)  Г É F; Г É Y 2) Г É FÙY 3) Г É FÙY 4) Г É F
Г É F; Г É Y 2) Г É FÙY 3) Г É FÙY 4) Г É F

 Г É FÙY Г É F Г ÉY Г ÉYÚY
Г É FÙY Г É F Г ÉY Г ÉYÚY
5) 
 Г É Y 6) Г,F É Y; Г,C É Y; Г É FÚC 7) Г,F É Y
Г É Y 6) Г,F É Y; Г,C É Y; Г É FÚC 7) Г,F É Y
Г É FÚY Г ÉY Г É YÉY



 8) Г É F;Г É F ÉY 9) Г, ù F É 10) Г É F;Г É ù F
8) Г É F;Г É F ÉY 9) Г, ù F É 10) Г É F;Г É ù F
 Г ÉY Г É F Г É
Г ÉY Г É F Г É
11) Г,F,Y, Г1 É C 12) Г É F

 Г, Y,F, Г1 É C Г, Y É F
Г, Y,F, Г1 É C Г, Y É F
Правила 1, 2 и 3, эксплуатируя сущность конъюнктивной связки, позволяют упростить модель теоремы.
Правила 4 и 5, эксплуатируя сущность дизъюнктивной связки, позволяют в заключении теоремы вводить новые дополнительные формулы.
Правило 6 формирует способ рассуждения «разбор» двух возможных случаев. Если при выполнении посылок Г справедливо Ф или Х, а Y справедливо при выполнении условий Г и Ф, а также при выполнении условий Г и Х, то Y всегда справедливо при выполнении посылок Г, что устанавливается путем рассмотрения двух возможных случаев:
а) выполнены условия Г и Ф;
б) выполнены условия Г и Х.
Правило 7 формализует прием эквивалентной перефор-мулировки теоремы, позволяющей одну из посылок теоремы помещать в заключение в виде посылки.
Правило 8 - правило вывода (отделения), modus ponens, введенное ещё Аристотелем. Оно указывает, как можно освобождаться от посылки в заключении.
Правило 9 - формализует «рассуждение от противного». Пусть, условие Г и ù Ф могут одновременно выполняться. Приходя к противоречию, заключаем, что из выполнимости Г всегда вытекает выполнимость Ф.
Правило 10 - это правило «обнаружения противоречия».
Правило 11 - перестановка посылок не влияет на истинность заключения.
Правило 12 - добавляя лишнюю посылку, мы не нарушаем истинность заключения теоремы.
Выводы: правила вывода 1-12 являются функционально полным набором правил, применяя которые к исходным аксиомам и доказанным теоремам, можно в конце концов получить доказательство истинного значения заключения в теореме - цели. Однако обязательными требованиями построения доказательства с помощью правил вывода 1-12 являются следующие:
1) исходными посылками должны быть только аксиомы и доказанные теоремы.
2) с помощью правил вывода 1-12 (и только этих правил) можно строить композиции аксиом и доказанных теорем, стремясь в итоге получить заключение теоремы-цели. Эти два требования соответствуют стереотипу классического дедуктивного рассуждения, иногда называемого прямой дедукцией, т.е. рассуждения от истинных абстрактных посылок (аксиом и доказанных теорем) к истинному конкретному заключению. Примеры несоблюдения требований:
а) Все металлы - элементы;
б) Бронза - металл
 Бронза - элемент
Бронза - элемент
Вывод ошибочен: бронза не является элементом. Здесь нарушен закон тождества, который запрещает в процессе данного умозаключения в одно и то же понятие вкладывать различное содержание. В посылках употреблен металл не в одинаковом смысле. В а) металл - химический элемент, а в б) - металл - это вещество, используемое в хозяйстве, производстве.
‚ Бэкон и Гоббс были египтянами
 Бэкон и Гоббс были идеалистами
Бэкон и Гоббс были идеалистами
Некоторые идеалисты были египтянами
Вывод в умозаключении верный, однако, обе посылки ложны: Бэкон и Гоббс были англичанами и материалистами.
Практика показала, что способ доказательства теорем прямой дедукцией чрезвычайно неэффективен по следующей причине. Структура композиций на промежуточных шагах преобразований является случайной в связи с тем, что не существует критериев и управляющих воздействий, которые целенаправленно ориентировали бы эти композиции к заданной цели. Поэтому не исключена возможность ухода в сторону от цели, что чаще всего и бывает на практике. Из этого вытекает глобальный вывод о неэффективности прямой дедукции при доказательстве теорем. В связи с этим правила 1-12 чаще всего используются для приведения структуры теоремы к канонической форме. Вернуться
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 553; Нарушение авторских прав?; Мы поможем в написании вашей работы!