Правила образования языка в алфавите (синтаксис)

Алфавит логики предикатов позволяет определить новые понятия, необходимые для языка этой логики.

Понятие «отношение». В логике предикатов предикат выражает взаимную связь отражаемых объектов со своими свойствами, характеристиками, действиями, взаимосвязь объектов, процессов, действий. Количество указанных предметов в одном отношении не ограничивается. Отношение может быть двухместным (т.е. между двумя предметами), трехместным, n-местным. Истинное высказывание является отношением. Формально самое распространенное двухместное отношение (бинарное) рассматривается как множество пар элементов и обозначается вектором <x,y>, где x называется первой, а y - второй координатой пары. Векторное представление n - мерных отношений тоже широко распространено.

Понятие «терм»- это всякая константа, предметная переменная и функция.

Понятие «функция» символизирует действие, ставящее в соответствие списку констант одну определенную константу. Всякая функция имеет определенное число аргументов. Если функциональный символ f имеет n-аргументов, то f - называется n - местным функциональным символом. Константа может рассматриваться как функциональный символ без аргументов.

Обозначение функции - f(t₁,t_2,...t_n),где t_i -термы; при n=0 функция обозначается просто f.

Примеры:

1) Плюс(t_1,t_2,t₃₎ означает t₁+t₂+t₃=t_å

2) Плюс(Плюс (t₁,t₂,t₃,t₄),Минус (t_5,tt₆),Умножить(t_1,...,t_n))

3) Отец(Отец(Иван)), что определяет дедушку Ивана.

Предикат - это обобщение понятия «высказывание», заключающееся:

1) в абстрагировании предметов, участвующих во взаимосвязях этого высказывания;

2) в обеспечении возможности внешнего управления внутренними взаимосвязями этого высказывания с помощью кванторных символов.

Всякий предикат имеет определенное число аргументов. Если предикатный символ P имеет n - аргументов, то он называется n - местным предикатным символом.

Обозначение - P(t_1,...,t_n), где t_i- термы; при n=0 предикат обозначают P вместо P().

Предикат символизирует действие, ставящее в соответствие списку констант одно из истинностных значений И или Л. Это значит, что предикат (как высказывательная форма) после замены в нем аргументов - предметных переменных конкретными константами превращается в высказывание, которое может быть или И, или Л. Истинный предикат называется отношением.

Так же, как и в высказывании, в предикате выражаются взаимосвязи между различными предметами: между отражаемым объектом и его свойствами, характеристиками и действиями, между парами или большим количеством объектов, процессов, явлений.

Предикатный символ, как правило, представляет сказуемое в повествовательном предложении, о котором можно сказать, истинно оно или ложно. Но очень часто в предикатном символе отражается семантика взаимосвязи отражаемых предметов.

Примеры:

1) ЛЮБИТ (Иван, Мария)

2) ЛЮБИТ (отец(Иван), Иван)

3) БОЛЬШЕ (х,3), где х R - множество натуральных чисел.

4) БОЛЬШЕ (плюс(х,1),х)

5) СТОЛИЦА (х,y)

где х {Москва, Киев, Минск},

y {Россия, Украина, Белоруссия}

6) СОДЕРЖАТЬ (x,y,v)

где х {углерод, сера},

y {сталь, кремний},

v {множество вещественных чисел}

7) ПОСТАВКА (x,y,z,i,j,k,l,m),

где х |чего?|{ список комплектующих},

y |кому?|{ список получателей},

z |кто?|{ список поставщиков},

i |откуда?|{ список источников},

j |куда?|{ список приемников},

k |сколько?|{ список кол-ва комплектующих},

l |по цене? |{ список цен}?

m |транспортные расходы?|{ список удельных стоимостей

перевозок}

8) ОБЛАДАТЬ СВОЙСТВАМИ И ХАРАКТЕРИСТИКАМИ (z,x₁,x₂,x₃,y₁,y₂,y₃),

где z |отражаемый объект?|{ список отражаемых объектов},

x₁ |цвет?|{ список цветов},

x₂ |запах?|{ список запахов},

x₃ |вкус?|{ список вкусов},

y₁ |геометрическая форма?|{ список геометрических форм},

y₂ |твердость?|{ список показателей твердости},

y₃ |удельный вес?|{ список удельных весов}.

Понятие «атом» - это предикат, представленный в виде формулы P(t₁,t₂,...,t_n)

Синтаксис языка определяется рекурсивно следующими правилами:

1) Атом есть формула

2) Если F и G - формулы, то (ùF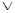),(FG),(FG),(F® G) и (F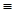G) - формулы.

3) Если F - формула, а x - предметная переменная F, то ()F и (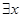)F - формулы.

4) формулы порождаются только конечным применением правил 1-3.

Область действия квантора - это та формула, к которой он применяется.

Например, областью действия квантора существования в формуле 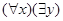МЕНЬШЕ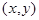есть формула МЕНЬШЕ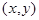,а область действия квантора всеобщности есть формула 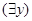МЕНЬШЕ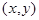. В формуле область действия квантора всеобщности есть формула .

Вхождение переменной 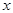в формулу называется связанным тогда и только тогда, когда оно совпадает с вхождением в кванторный комплекс 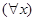или 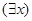, или находится в области действия такого комплекса.

Вхождение переменной в формулу свободно тогда и только тогда, когда оно не является связанным.

Например, в формуле 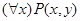переменная 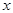связана, т.к. оба вхождения 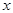связаны. Однако, переменная 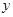свободна, т.к. единственное вхождение 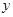свободно.

Переменная в формуле может быть свободной и связанной, например, переменная 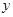и свободна, и связана в формуле .

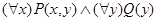Понятие «семантика квантора всеобщности 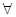». Квантор всеобщности 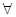устанавливает правило интерпретации формулы F, к которой он применяется. При каждом конкретном значении переменной 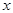(которую квантор 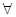связывает в формуле F), принадлежащем области определения переменной 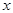, формула F, как функция от 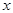, может принимать или только истинные значения, или только ложные, но совмещение И и Л недопустимо на всей области определения.

Понятие «семантика квантора существования 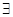». Квантор существования 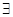устанавливает правило интерпретации формулы F, к которой он применяется. Хотя бы при одном конкретном значении переменной 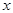(которую 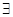связывает в формуле F), принадлежащем области определения 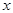, формула F, как функция от 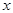, обязательно принимает истинное (или ложное) значение.

Пример рассуждения, записанного языком логики предикатов.

1) каждый человек смертен.

2) Конфуций - человек, следовательно, Конфуций - смертен.

«X - есть человек» обозначим через ЧЕЛОВЕК,

«X - смертен», через СМЕРТЕН.

Первое утверждение представим формулой:

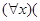ЧЕЛОВЕК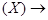СМЕРТЕН.

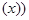Утверждение «Конфуций - человек» - это формула ЧЕЛОВЕК (Конфуций), а «Конфуций - смертен» - формула СМЕРТЕН (Конфуций). В целом рассуждение представляется формулой:

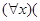ЧЕЛОВЕК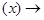СМЕРТЕН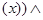ЧЕЛОВЕК(Конфуций)

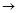СМЕРТЕН(Конфуций).

Дата добавления: 2014-01-04