
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правила присваивания истинностных значений
|
|
|
|
формулам (семантика языка).
Чтобы определить интерпретацию для формулы логики предикатов следует задать:
n общую область определения D для всех предметных переменных, входящих в формулу;
n значения констант;
n истинностные значения предикатов, входящих в формулу;
n значения функций, входящих в формулу
При этом:
1) каждой константе ставится в соответствие некоторый элемент из D;
2) каждому n-местному функциональному символу ставится в соответствие отображение из Dn в D (заметим, что Dn=
3) каждому n-местному предикатному символу ставится в соответствие отображение Dn в множество {И,Л}.
Для каждой интерпретации формулы из области D формула может получать истинностное значение И или Л согласно следующим правилам:
1. если заданы значения формул G и H, то истинностные значения формул ùG,(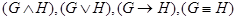 ) получаются по табл. 2 логики высказываний.
) получаются по табл. 2 логики высказываний.
2. 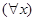 G получает значение И, если G получает значение И для каждого x из D; в противном случае она получает значение Л.
G получает значение И, если G получает значение И для каждого x из D; в противном случае она получает значение Л.
3. 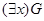 получает значение И, если g получает значение И хотя бы для одного x из D;в противном случае она получает значение Л.
получает значение И, если g получает значение И хотя бы для одного x из D;в противном случае она получает значение Л.
4. Формула, содержащая свободные переменные, не может получить истинностное соглашение. В логике предикатов действует следующее соглашение: формула либо не содержит свободных переменных, либо свободные переменные рассматриваются как константы.
Пример: Оценим формулы
а) 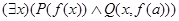
b) 
c) 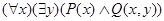
в следующей интерпретации I:
 Л,
Л, 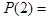 И,
И, 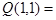 И,
И,
 И,
И, 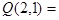 Л,
Л, 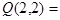 И.
И.
Для формулы а): если 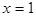 , то
, то
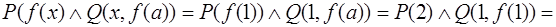
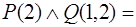 И
И И = И;
И = И;
если 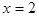 , то
, то

Л Л = Л.
Л = Л.
Так как в области D существует элемент, а именно 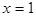 , такой, что
, такой, что 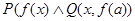 истинна, то а) истинна при интерпретации I.
истинна, то а) истинна при интерпретации I.
Для формулы b):
если 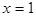 , то
, то
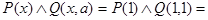 Л
Л И
И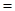 Л;
Л;
если x=2, то
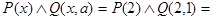 И
И Л
Л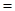 Л.
Л.
Т. к. в D не существует такого элемента, что 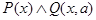 истинна, что формула b),будет ложной при интерпретации I.
истинна, что формула b),будет ложной при интерпретации I.
Для формулы c):
если 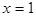 , то
, то  Л. Следовательно,
Л. Следовательно,  = Л для
= Л для  и для
и для  . Так как существует
. Так как существует  , а именно
, а именно 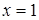 , такой, что
, такой, что 
 ложно, то формула с) ложна при интерпретации I, т.е. эта формула опровергается интерпретацией I.
ложно, то формула с) ложна при интерпретации I, т.е. эта формула опровергается интерпретацией I.
Определим ряд важнейших понятий для логики предикатов.
Непротиворечивая (выполнимая) формула - формула G выполнима (непротиворечива) тогда и только тогда, когда существует такая интерпретация I, что G имеет значение И в I. Если формула G есть И в интерпретации I, то I есть модель формулы G и I удовлетворяет G.
Противоречивая формула – когда не существует никакой интер-претации, которая удовлетворяет G.
Общезначимая формула – когда не существует никакой интер-претации I, которая не удовлетворяет G.
Логическое следствие – формула G есть логическое следствие формул 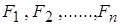 тогда и только тогда, когда для каждой интерпретации I, если
тогда и только тогда, когда для каждой интерпретации I, если 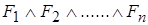 истинна в I, то G также истинна в I.
истинна в I, то G также истинна в I.
Замечание: Так как в логике предикатов количество областей определения предметных переменных ничем не ограничивается, т.е. их может быть бесконечное число, то имеется бесконечное число интерпретаций формулы. Следовательно, в отличие от логики высказываний, отсутствует возможность доказательства общезначимости или противоречивости формулы путем определения ее истинностных значений при всех возможных интерпретациях, даже в самых простых случаях. Поэтому доказательство теорем (достоверности рассуждений) в логике предикатов осуществляется только методом резолюций, однако имеющем свои особенности. Вернуться
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 280; Нарушение авторских прав?; Мы поможем в написании вашей работы!