Вычисление двойного интеграла в прямоугольных координатах

По определению:

Пусть граница области интегрирования задана уравнением . Выразив из этого уравнения одну переменную через другую, найдемявные уравнения линий, ограничивающих область интегрирования слева- X_лев(y) и справа X_пр(y) или сверху У_В (х) и снизу У_Н(х).

Пользуясь произвольностью разбиения и выбора отмеченных точек в ячейках разбиения,

- введем разбиение области интегрирования D линиями координатной сетки

y=y_j=const ||OX - и x=x_i=const ||OY

на прямоугольные «ячейки» площадью и

- внутри каждого, например, вертикального «столбца» x_i<x<x_i+1 выберем отмеченные точки с одинаковыми абсциссами: x=x_i^*.

x_i+1

x_i

- упорядочим суммирование в интегральной сумме

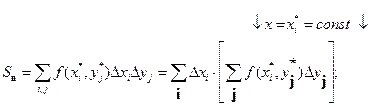
Очевидно, что внутренняя сумма представляет интегральную сумму (1) для интеграла от функции одной переменной 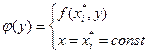, которая при измельчении разбиений
определяет «определенный интеграл» по промежутку [y_H(x_i); y_B y_H(x_i)]

После этого, внешняя сумма 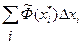так же представляет интегральную сумму (1) для интеграла от функции одной переменной :

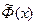Таким образом, вычисление двойного интеграла в прямоугольных координатах сводится к двукратному интегрированию функции f(x,y), при этом

(1) внутреннее интегрирование функции одной переменной выполняется в области D вдоль прямой или . Пределы этого интегрирования – уравнения линий, ограничивающих область D СНИЗУ () и СВЕРХУ (y=или СЛЕВА 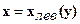и СПРАВА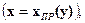

(2) повторное интегрирование (внешний интеграл) функции одной (второй) переменной выполняется по отрезку 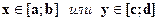, где a,b и c,d - наименьшее и наибольшее значения соответствующих переменных на всей области интегрирования D.

-----------------------------------------------------------------------

ЭКЗ Показать, что

-----------------------------------------------------------------------

Замечание. Если при выбранном порядке интегрирования границы области вдоль соответствующей «координатной прямой» задаются различными уравнениями (“сложная область”), область интегрирования следует разбить на “ простые для выбранного порядка интегрирования» части: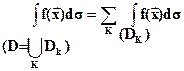

Алгоритм вычисления двойного интеграла в прямоугольных координатах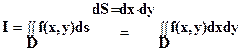

(1) Выбрать «порядок интегрирования» и записать двойной интеграл в виде двукратного: .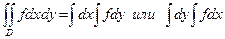

(2) Представить область интегрирования D в виде объединения частей D_i, простых для выбранного порядка интегрирования, и записать интеграл как сумму двукратных интегралов:

(3) Для каждой «простой» области D_i записать в явном виде уравнения границ вдоль соответствующей координатной линии, проставить пределы интегрирования и вычислить двукратный интеграл.
--------------------------------------------------------------------------

ПРИМЕР.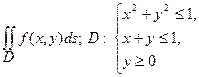

(1)

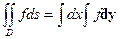
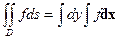
(2) x=const è y=const è D– «простая» область

(3) вдоль линии x=const ||OY вдоль линии y=const ||OX

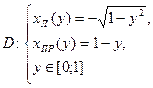
Дата добавления: 2014-01-04