Интерференция световых волн. Основное уравнение интерференции. Интерференционное поле от двух точечных источников. Опыт Юнга

Рассмотрим две волны одинаковой частоты, которые, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления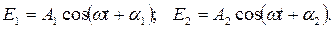

Амплитуда результирующего колебания в данной точк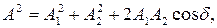е где .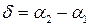

Если разность фаз 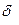возбуждаемых волнами колебаний остается постоянной во времени, волны называются когерентными. В случае некогерентных волн 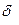непрерывно меняется, принимая с равной вероятностью любые значения, поэтому среднее за период значения 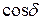равно нулю и

-

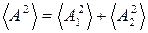интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой волной в отдельности: .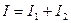

В случае когерентных волн 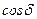имеет постоянное во времени, но свое для каждой точки пространства, значение, и

.

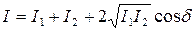В точках пространства, где 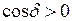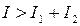, в точках, где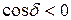 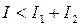. Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн. Если интенсивности обеих волн одинаковы, то в максимумах 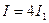, а в минимумах 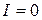. Для некогерентных волн в этом случае интенсивность равна .

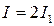Естественные источники не дают когерентного света. Это связано с тем, что излучение светящегося тела слагается из волн, испускаемых многими атомами. Излучение производится цугами длиной до 3м, причем 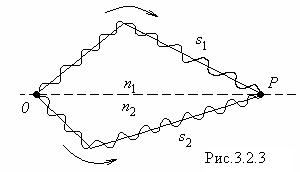фаза одного цуга никак не связана с фазой следующего.

Когерентные волны можно получить, разделив волну, излучаемую одним источником, на две части (рис.3.2. 3). Если заставить эти волны пройти разные оптические пути, а потом наложить друг на друга, наблюдается интерференция. Разность оптических путей, проходимых волнами, не должна быть очень большой, чтобы складываемые колебания принадлежали одному цугу волн.

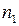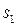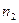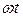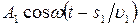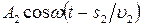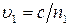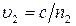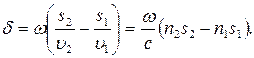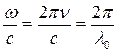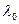Пусть разделение волн происходит в точке Р. До точки Р первая волна проходит в среде с показателем преломления путь , вторая волна – в среде с показателем преломления путь . Если в тоске О фаза колебаний равна , то первая волна возбудит в точке Р колебание , а вторая волна – колебание , где , - фазовые скорости волн. Разность фаз возбуждаемых в точке Р колебаний, равна Заменив , где - длина волны в вакууме, имеем 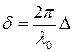, где 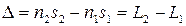- оптическая разность хода.

Если оптическая разность хода равна целому числу длин волн в вакууме,

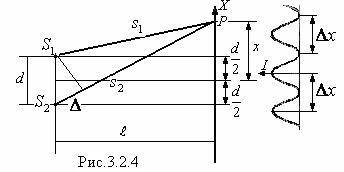
(т = 0,1,2….), (3.2.1)

то разность фаз 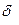будет кратна 2 π, и колебания, возбуждаемые в точке Р обеими волнами, будут происходить в одной фазе, т.е. (3.2.1) – условие максимума интерференции.

Если 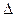равна полуцелому числу длин волн в вакууме,

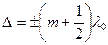(т = 0,1,2….), (3.2.2)

то 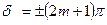, и колебания в точке Р будут в противофазе, т.е. (3.2.2) – условие минимума интерференции.

Рассмотрим две цилиндрические когерентные световые волны, исходящие из источников 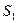и 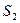(опыт Юнга), имеющих вид параллельных тонких светящихся нитей (рис.3.2. 4). Область, в которой эти волны перекрываются, называется полем интерференции. Во всей этой области наблюдается чередование максимумов и минимумов интерференции. Если в поле интерференции внести экран, на нем будет видна интерференционная картина, имеющая вид чередующихся темных и светлых полос. Вычислим ширину этих полос, если экран параллелен плоскости, проходящей через источник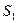и и 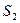. Положение точки на экране будем характеризовать координатой х, отсчитываемой в направлении, параллельном прямой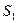 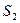, начало отсчета выберем в точке О, относительно которо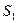й и 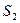расположены симметрично. На рис.3.2.4

Тогда

Для получения различимой интерференционной картины расстояние между источниками d должно быть значительно меньше расстояния до экрана 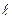. Расстояние х, в пределах которого образуются интерференционные полосы, также много меньше 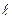. Тогда 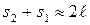, и 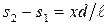. Умножив 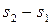на показатель преломления среды п, получим оптическую разность хода

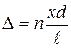. (3.2.3)

Подставив (3.2.3) в (3.2.1) и (3.2.2), получаем координаты максимумов и минимумов на экране:

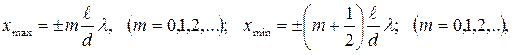
где 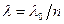- длина волны в среде. Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между двумя соседними минимумами – шириной интерференционной полосы. Эти расстояния имеют одинаковые значения

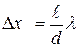. (3.2.4)

Согласно (3.2.4), расстояние между полосами растет с уменьшением расстояния между источниками d. При d, сравнимом с 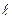, расстояние между полосами было бы того же порядка, что и 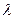. В этом случае отдельные полосы были бы совершенно неразличимы. Чтобы интерференционная картина была отчетливой, необходимо, чтобы .

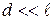Если интенсивность интерферирующих волн одинакова, 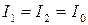, то результирующая интенсивность в точках с разностью фаз 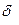равна

.

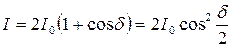Т.к. 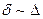, то согласно (3.2.3), 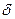растет пропорционально х. Следовательно, интенсивность меняется вдоль экрана по закону квадрата косинуса.

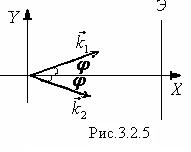Ширина интерференционных полос и расстояние между ними зависят от длины волны 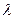. Только в центре картины, при х =0, совпадают максимумы всех длин волн. По мере удаления от центра максимумы разных цветов смещаются друг относительно друга все больше и больше. Интерференционная картина смазывается.

Рассмотрим интерференцию двух плоских волн одинаковых амплитуд. Направления распространения этих волн образуют угол 2 φ (рис.3.2.5). Направления колебаний светового вектора будем считать перпендикулярными к плоскости рисунка. Волновые векторы и 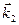лежат в плоскости рисунка и равны по модулю 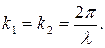Уравнения этих волн

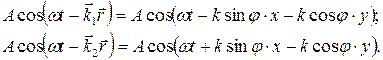
Результирующее колебание в точке с координатами х, у

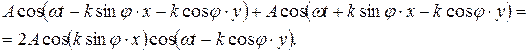
Из этого выражения следует, что в точках, где 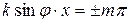(т = 0,1,2,…), амплитуда колебаний равна 2 А; в точках, где 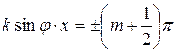(т = 0,1,2,…), амплитуда колебаний равна нулю. Где бы ни был экран Э, перпендикулярный оси 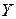, на нем будет наблюдаться система чередующихся светлых и темных полос, параллельных оси Z. Координаты максимумов интенсивности

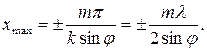
От положения экрана (от у) зависит лишь фаза колебаний.

Дата добавления: 2014-01-04