Роль когерентности. Временная (продольная) когерентность. Пространственная (поперечная) когерентность

Когерентностью называется согласованное протекание нескольких колебательных или волновых процессов. Различают пространственную и временную когерентность.

Волновое число связано с частотой соотношением 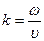. Поэтому разбросу частот 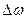соответствует разброс значений k, и временная когерентность обусловлена разбросом значений k, пространственная когерентность связана с разбросом направлений вектора .

Рассмотрим временную когерентность. Монохроматическая волна описывается выражением

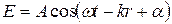
и, строго говоря, является абстракцией. Всякая реальная световая волна образуется наложением колебаний разных частот, заключенных в интервале конечной ширины 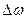. Амплитуда волны А и фаза 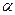претерпевают со временем случайные изменения, поэтому колебания, возбуждаемые в некоторой точке пространства двумя накладывающимися друг на друга световыми волнами, имеют вид

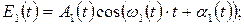
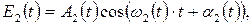
причем хаотические изменения функций 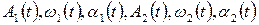являются совершенно независимыми.

Будем считать амплитуды 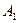и постоянными. Изменения частоты и фазы можно свести либо к изменению одной частоты, либо к изменению одной фазы. Действительно, представим функцию в ви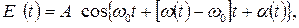де где - некоторое среднее значение частоты. Обозначим 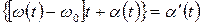. Тогда 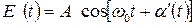, мы получили функцию, у которой хаотические изменения претерпевает лишь фаза колебаний.

С другой стороны, любую негармоническую функцию, например, , можно представить в виде суммы гармонических функций с частотами, заключенными в интервале частот .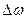

Таким образом, при рассмотрении вопроса о когерентности возможны два подхода – фазовый и частотный. Рассмотрим фазовый подход. Пусть частоты накладываемых волн одинаковы и постоянны, 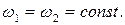Выясним влияние изменения фаз на процесс интерференции волн. Интенсивность света в любой точке определяется выражением

где Выражение 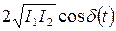называется интерференционным членом.

Всякий прибор, с помощью которого можно наблюдать интерференцию (глаз, фотопластинка и др.), обладает некоторой инерционностью и регистрирует картину, усредненную по некоторому промежутку времени 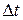. Если за время 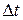множитель 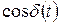принимает все значения от +1 до –1, среднее значение интерференционного члена будет равно нулю, и регистрируемая прибором интенсивность будет равна сумме интенсивностей, создаваемых каждой волной в данной точке, интерференции не будет. Если за время 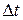значение 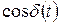изменяется мало, прибор обнаружит интерференцию.

Фаза волны, образованной наложением огромного числа цугов, порождаемых отдельными атомами, не претерпевает больших скачков, а изменяется случайным образом небольшими скачками. Время , за которое случайное изменение фазы волны 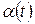достигает значения порядка , называется временем когерентности. За это время колебание как бы забывает свою первоначальную фазу и становится некогерентным по отношению к самому себе.

Расстояние , на которое перемещается волна за время когерентности, называется длиной когерентности или длиной цуга. Это расстояние, на котором случайное изменение фазы достигает значения порядка . При делении естественной волны для получения интерференционной картины необходимо, чтобы оптическая разность хода была меньше длины когерентности. Это требование ограничивает число видимых интерференционных полос. С увеличением номера полосы т разность хода растет, а четкость ухудшается.

Выясним роль немонохроматичности световых волн. Пусть свет состоит из последовательности идентичных световых цугов частоты 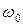и длительности . При смене одного цуга другим фаза претерпевает беспорядочные изменения, вследствие этого цуги оказываются некогерентными. В этом случае длительность цуга 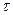совпадает со временем когерентности. Можно показать, что длительность цуга пропорциональна величине частотного интервала цуга Тогда время когерентности Чем шире интервал частот, представленных в данной световой волне, тем меньше время 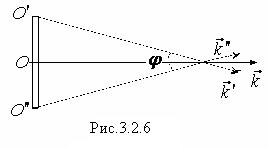когерентности. Частота связана с длиной волны 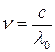, продифференцировав, получаем . Тогда время когерентности , и длина когерентности . Разность хода, при которой получается максимум т - го порядка, определяется соотношением . Когда эта разность хода достигает порядка длины когерентности, полосы становятся неразличимыми. Предельный наблюдаемый порядок интерференции находим из условия и 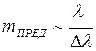. Таким образом, число наблюдаемых интерференционных полос возрастает при уменьшении интервала длин волн, представленных в используемом свете
.

Рассмотрим пространственную когерентность. Разброс вектора 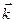будем характеризовать вектором . Возникновение в некоторой точке пространства колебаний, возбуждаемых волнами с разными 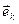, возможно, когда эти волны испускаются разными участками протяженного (неточечного) источника. Пусть источник имеет форму диска, видимого из данной точки под углом j. Из рис. 3.2.6 видно, что угол j характеризует интервал, в котором заключены орты . Будем считать этот угол малым.

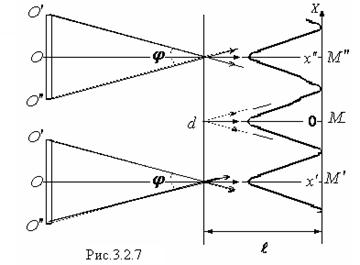
Допустим, что свет падает от источника на две узкие щели, за которыми находится экран (рис. 3.2.7). Интервал частот, испускаемых источником, мал, поэтому степень временной когерентности достаточна для получения четкой интерференционной картины. Волна, вышедшая из участка поверхности О (на рис. 3.2.7), создает нулевой максимум М в середине экрана. Нулевой максимум 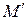, созданный волной, пришедшей от участка , будет смещен от середины экрана на расстояние 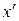. Угол j и отношение малы, поэтому 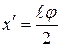. Нулевой максимум 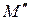, созданный волной, пришедшей от участка 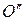, смещен от середины экрана в противоположную сторону на расстояние . Нулевые максимумы от остальных участков располагаются между максимумам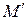и и.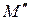

Отдельные участки источника света возбуждают волны, фазы которых никак не связаны между собой, поэтому интерференционная картина, наблюдаемая на экране, будет наложением картин, создаваемых каждым из участков в отдельности. Если смещение 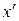много меньше ширины интерференционной полосы , максимумы от разных участков источника практически наложатся друг на друга, и картина будет такой же, как от точечного источника. При максимумы от одних участков придутся на минимумы от других, интерференционной картины не будет. Таким образом, интерференционная картина будет различимой при условии, что , т.е. или

. (3.2.5)

Здесь множитель 2 можно опустить.

Выражение (3.2.5) определяет угловые размеры источника, при которых наблюдается интерференция. Наибольшее расстояние между щелями, при котором еще наблюдается интерференция от источника с угловым размером j найдем, умножив (3.2.5) на :

(3.6)

Совокупность волн с разными можно заменить результирующей волной, падающей на экран со щелями. Отсутствие интерференционной картины означает, что колебания, вызванные этой волной в местах нахождения первой и второй щелей, некогерентны, т.е. и колебания в самой волне в точках, находящихся на расстоянии d друг от друга, не являются когерентными. Если бы источник был идеальным монохроматическим (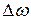=0), поверхность, проходящая через щели, была бы волновой, и колебания во всех точках этой поверхности происходили бы в одной фазе.

Поверхность, которая была бы волновой при условии монохроматичности источника, называют псевдоволновой. Колебания, возбуждаемые волной в достаточно близких точках псевдоволновой поверхности, будут когерентными. Такая когерентность называется пространственной.

Фаза колебаний при переходе от одной точки псевдоволновой поверхности к другой меняется случайным образом. Расстояние , при смещении на которое вдоль псевдоволновой поверхности случайное изменение фазы достигает значения порядка p, называется длиной или радиусом когерентности. Согласно (3.2.6),

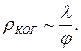
Колебания в двух точках псевдоволновой поверхности, отстоящих на расстояние, меньшее, будут когерентны.

Все пространство, занимаемое волной, можно разбить на части, в каждой из которых волна приблизительно сохраняет когерентность. Объем такой части пространства называется объемом когерентности. Он по порядку величины равен произведению длины временной когерентности на площадь круга радиуса .

Дата добавления: 2014-01-04