Интерференция в тонких пленках

Рассмотрим плоскопараллельную тонкую пластинку толщиной h (рис.3.2.11). На эту пластинку под углом i падает монохроматическая волна. По обе стороны от пластинки находится одна и та же среда с абсолютным показателем преломления n ₁. Абсолютный показатель преломления пластинки n ₂ (n ₂> n ₁). АВ – фронт падающей волны, АВ перпендикулярен к падающим лучам 1 и 2. Падающая волна частично отражается от верхней поверхности пластинки, и частично преломляется. Направление распространения отраженной волны 1', преломленной – 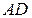. Преломленная волна, придя на нижнюю границу пленки, частично отражается (DС), и частично преломляется.

То же самое и на верхней границе: DС частично преломляется и проходит в среду, совпадая с лучом 2' (луч 1"). Эти волны, обусловленные отражением от верхней и нижней границ пленки, когерентны между собой. Результат их интерференции зависит от разности фаз 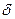,приобретенной в пленке.

В точках А и В фронта падающей волны колебания совершаются в одной фазе. Колебание в точке С, вызванное отраженной волной, отстает по фазе от колебаний в точке А на величину 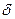₁=2 p (AD+DC)/ l ₂, где l ₂ – длина волны света в пленке.

Колебания в точке С, вызванные отраженной от верхней поверхности пленки волной, отстают по фазе на 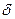₂=(2p BC/ l₁)+p, где l₁ – длина волны в среде, p учитывает сдвиг фаз при отражении света от оптически более плотной среды. Он эквивалентен дополнительному пути l ₁/2. Тогда разность фаз:

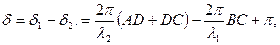
но _, l – длина волны в вакууме. Следовательно:

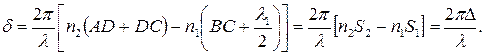Тогда условия максимума интерференции: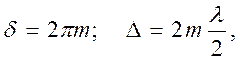

условия минимума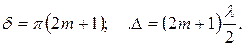

Для плоскопараллельной пленки имеем:

Тогда оптическая разность хода

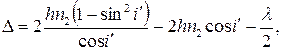По закону преломления света следовательно или 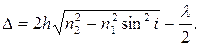Результат интерференции зависит от при имеет место максимум в отраженном свете, при - минимум.

Мы рассмотрели случай, когда на плоскопараллельную тонкую пластинку падает плоская волна. Рассмотрим интерференцию света при падении на пластинку расходящегося пучка лучей, соответствующего сферической волне (рис.3.2.12). Лучи 1, 2, 3 падают на пластинку под углами . Пары лучей 1', 1", 2', 2"; 3', 3" обусловлены отражением света от верхней и нижней поверхности пленки. Оптические разности хода между этими парами лучей неодинаковы, так как различны углы их падения. Для наблюдения интерференции в отраженном свете используют собирающую линзу Л и экран Э, расположенный в фокальной плоскости линзы. В каждой точке экрана собираются и интерферируют все лучи, которые после

отражения от пленки параллельны прямой, соединяющей эту точку с оптическим центром линзы О. Линза не создает дополнительной разности фаз между лучами. При освещении плоскопараллельной пленки

монохроматическим светом, результаты интерференции отраженного света в различных точках экрана зависят только от углов 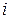падения на пленку. Интерференционная картина имеет вид чередующихся криволинейных темных и светлых полос, каждая из этих полос соответствует своему углу , полосы называется полосами равного наклона. Если оптическая ось линзы Л перпендикулярна к поверхности пленки, полосы равного наклона имеют вид концентрических окружностей с центром в главном фокусе линзы. Это явление используется для контроля плоскопараллельности пленок.

Рис.3.2. 14

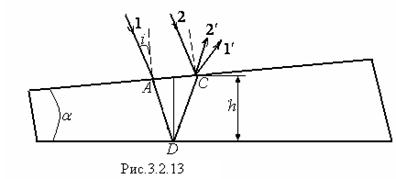
Рассмотрим интерференцию в больших пленках, толщина которых неодинакова в разных местах. Пусть пленка имеет форму клина с углом a между боковыми гранями. На клин падает плоская волна, направление которой совпадает с лучами 1 и 2 (рис.3.2.13). Направление распространения интерферирующих волн, которые возникают в результате отражения от верхней и нижней границ, соответствуют 1' и 2". Каждому значению соответствует одинаковая разность хода D, следовательно, одинаковые и результаты интерференции. Поэтому в отраженном свете наблюдаются полосы равной толщины.

Верхняя и нижняя грани клина не параллельны между собой, поэтому отраженные лучи 1' и 2' имеют разные направления и пересекаются только в точках верхней поверхности клина. Полосы равной толщины локализованы на поверхности клина.

Ширина интерференционной полосы для полос равной толщины

.

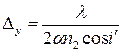Частным случаем полос равной толщины являются кольца Ньютона (рис.3.2. 14). Плосковыпуклая линза Л с большим радиусом кривизны выпуклой поверхности обращена выпуклой стороной к плоской пластинке А и соприкасается с ней в точке О. Параллельный пучок света падает нормально на плоскую поверхность ВС линзы и частично отражается от верхней и нижней поверхностей воздушного промежутка между линзой и пластиной. При наложении отраженных волн возникают интерференционные кольца равной толщины. В центре находится темное кольцо (минимум нулевого порядка). Оно окружено системой чередующихся светлых и темных колец, ширина и интенсивность которых постепенно убывают по мере удаления от центрального пятна. В проходящем свете наблюдается обратная картина – центральное пятно светлое, следующее кольцо темное, и т.д.

Оптическая разность хода между лучами, отраженными от верхней и нижней поверхностей воздушного зазора на произвольном расстоянии r=DE от точки О, равна 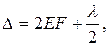показатель преломления воздуха принят равным единице, учитывает сдвиг фаз на p при отражении света от поверхности пластины. Из подобия прямоугольных треугольников EOD и EDM имеем

где 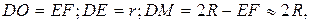так как Тогда и 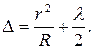Подставив это выражение в условия максимумов и минимумов интерференции, получаем радиусы т -ных светлого 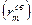и темного 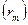колец Ньютона в отраженном свете:

В проходящем свете

Рис. 3.2.15 Рис.3.2.16

Правильная форма колец Ньютона легко искажается при всяких, даже незначительных дефектах в обработке выпуклой поверхности линзы и верхней поверхности пластины. Поэтому наблюдение колец Ньютона позволяет осуществить быстрый и весьма точный контроль качества шлифовки плоских пластин и линз, а так же близость их поверхностей к сферической форме.

Дата добавления: 2014-01-04