
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Малые деформации
|
|
|
|
 |
Аналогично напряжениям деформации изменяются от точки к точке деформируемого тела, поэтому соотношения между деформациями определяются для малого объема тела. Выделим в теле плоскостями, параллельными координатам, бесконечно малый параллелепипед с ребрами dx, dy, ' dz (рис. 12).
. При деформации параллелепипед перемещается, длина его ребер и прямые в исходном состоянии углы между гранями изменяются. При этом наблюдается деформация двух видов — линейная (удлинение или укорочение) и угловая (сдвиг).
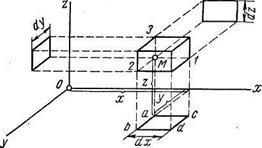
Величина малых относительных линейных деформаций определяется отношением приращения длины ребра к исходной длине и обозначается е с индексом, указывающим наппявление оси, параллельно которой ребро получило удлинение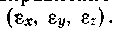
|
| Рис. 13. Параллелепипед и его проекции до деформации |

|
Рис. 14. Проекция параллелепипеда на плоскость хОу до деформации и в момент деформации
Величина относительной деформации сдвига определяется углом между направлениями ребер в исходном состоянии и после деформации и обозначается с двумя индексами:
с двумя индексами: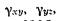
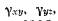
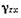
 и т. д. Первый индекс указывает направление оси, параллельно которой ребро находилось в исходном состоянии, а второй — ось, по направлению к которой повернулось ребро (см. рис. 12).
и т. д. Первый индекс указывает направление оси, параллельно которой ребро находилось в исходном состоянии, а второй — ось, по направлению к которой повернулось ребро (см. рис. 12).
Определим составляющие деформации в функции перемещений. Выделим в деформируемом теле бесконечно малый параллелепипед с ребрами  (рис. 13). Рассмотрим проекцию этого параллелепипеда на координатную плоскость
(рис. 13). Рассмотрим проекцию этого параллелепипеда на координатную плоскость  (рис. 13 и 14). Проекция параллелепипеда до деформации
(рис. 13 и 14). Проекция параллелепипеда до деформации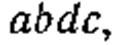 а после деформации
а после деформации  . Перемещение точки а в направлении оси х обозначим через и, в направлении оси
. Перемещение точки а в направлении оси х обозначим через и, в направлении оси  , через v и в направлении оси
, через v и в направлении оси  через
через 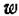 . Смещение точки С в направлении оси х, пренебрегая членами второго и высшего порядка малости, равно
. Смещение точки С в направлении оси х, пренебрегая членами второго и высшего порядка малости, равно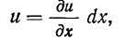 где
где 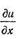 — интенсивность развития функции Ũ в направлении х
— интенсивность развития функции Ũ в направлении х

|
— приращение перемещения u на длине dx /
Относительное удлинение ребра ас, равного до деформации dx, можно
выразить так (рис. 14):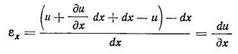
|
Аналогично для относительного удлинения ребра вдоль оси y получаем
 |
При деформации ребра параллелепипеда, параллельные осям координат в исходном состоянии, не будут им параллельны, так как произойдет поворот их в результате деформаций сдвига. Деформация сдвига в плоскости хОу равна сумме углов
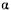 и β поворота ребер аb и ас:
и β поворота ребер аb и ас: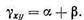
|
Угол поворота ребра ас определим из треугольника а1с1с2: tg β = c1c2 / а1с2
Перемещение точки С в положение C1 в направлении оси у равно 
 интенсивность развитая функции v в направлении оси х, а произведение — приращение перемещения
интенсивность развитая функции v в направлении оси х, а произведение — приращение перемещения  на длине
на длине 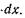 Отсюда
Отсюда
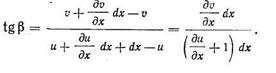
|
Так как мало по сравнению с единицей и при малых деформациях можно принять
мало по сравнению с единицей и при малых деформациях можно принять получаем
получаем 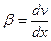
Аналогично определяем угол ά

Итак, деформация сдвига
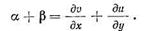
|
Проектируя параллелепипед (см. рис. 13) на координатные плоскости 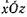 и
и 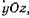 , определяем линейные деформации
, определяем линейные деформации 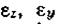 и деформации сдвига. В результате получаем следующие дифференциальные зависимости малых деформаций от перемещений:
и деформации сдвига. В результате получаем следующие дифференциальные зависимости малых деформаций от перемещений:
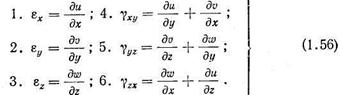
В шести уравнениях (1.56) имеется девять неизвестных. Для решения этих уравнений и нахождения всех неизвестных нужно записать еще 3 уравнения неразрывности связи линейных деформаций и деформаций сдвига.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1307; Нарушение авторских прав?; Мы поможем в написании вашей работы!