Понятие о тензоре деформаций

Деформированное состояние в точке определяется девятью составляющими — тремя линейными деформациями и

шестью деформациями сдвига:

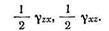
Составляющие деформации в точке можно расположить в следующей таблице:

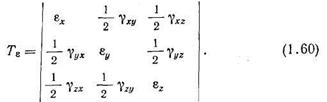
Деформированное состояние в точке вполне определено, если для нее задан тензор деформации. Тензор деформации обладает теми же свойствами, что и тензор напряжений, поэтому все формулы в теории деформации можно записать по аналогии с соответствующими формулами теории напряже­ний

В каждой точке тела существуют три взаимно перпендику­лярных направления, которые называют главными осями де­формации, КОТОРЫЕ обладают тем свойством, что «волокна в теле, параллельные им, испытывают только линейные деформации (укорачиваются или удлиняются), но не поворачи­ваются, т. е. сдвиги в главных осях деформации равны нулю. Главные линейные деформации обозначают с индексами 1, 2, 3:

Тензор деформации можно разложить на шаровой тензор

ε_ср 0 0

0 ε_ср 0

0 0 ε_ср

и девиатор тензора деформации

ε₁ - ε_ср 0 0 ε₁ 0 0

D _ε = 0 ε₂ - ε_ср 0 = 0 ε₂ 0

0 0 ε₃ - ε_ср 0 0 ε₃

Составляющие шарового тензора при пластической де­формации равны нулю. Следовательно, тензор деформации при пластической деформации является девиатором.

Ин­варианты тензора деформации записываются так: первый инвариант — линейный:

(1.63)

второй инвариант квадратичный:

третий инвариант — кубический:

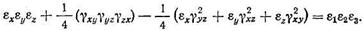
По аналогии с напряжениями введем понятие средней линей­ной деформации:

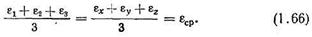
Т.к. величина средней линейной деформации ε_ср. = 0, то и линейный инвариант тензора дефор­мации равен нулю.

2.4 Большие деформации. Особенность деформации металла при обработке давлением.

Процессы обработки металлов давлением характеризуются большим разнообразием (рис.2.1) и отличаются между собой по форме и типу применяемых заготовок (слитки, болванки, листовая заготовка и т. п.), по форме и характеру движения инструмента (возвратно-поступательное или вращательное), по типу деформации (пластическая или с разрушением металла), по схемам действующих сил (растягивающие, сжимающие и их комбинации) и по форме получаемых изделий.

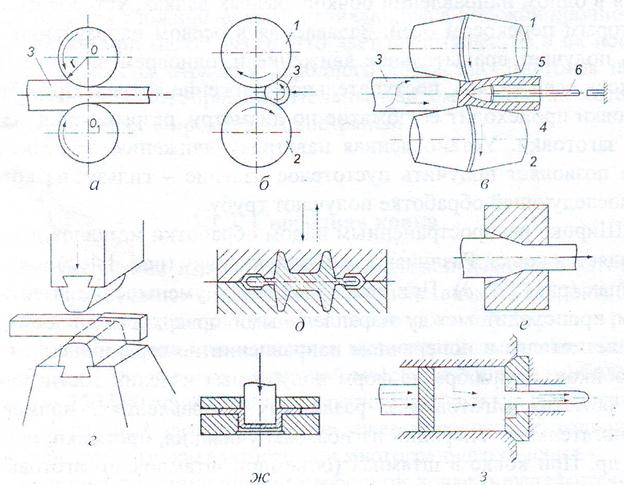
Рис. 2.1. Схемы основных технологических процессов обработки металлов давлением: прокатка продольная (а), поперечная (б), поперечно-винтовая (в) (1, 2 – валки, 3 – заготовка, 4 – гильза, 5 – оправка, 6 – стержень оправки); свободная ковка (г), горячая штамповка (д), волочение (е), листовая штамповка (ж), прессование (з).

Для процессов ОМД характерны большие (конечные) пластические деформации при различных температурах и скоростях нагружения, а поскольку плотность деформируемого металла изменяется незначительно (не более нескольких долей процента), то принимается условие – ЗАКОН постоянства объема, которое, например, для осадки прямоугольного тела высотой h ₀, шириной b ₀ и длиной l ₀ записывается так:

h ₀ b ₀ l ₀ = h ₁ b ₁ l ₁ (2.1)

где h ₁, b ₁ и l ₁ соответственно высота, ширина и длина сторон прямоугольника после деформации.

При обработке давлением в процессе деформации размеры тела значительно изменяются, поэтому принято абсолютную деформацию за малый промежуток времени относить к размеру тела в начальный момент этого промежутка, например, при осадке тела с начальной высоты h ₀ до конечной высоты h ₁ бесконечно малое изменение (уменьшение) его высоты равно dh бесконечно малая деформация будет равна

d δ _h = 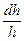и тогда полная относительная деформация определится как сумма малых деформаций за весь процесс деформации δ _h = 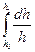= ln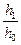, аналогично деформации в направлениях ширины b ₁ и l ₁ и длины l ₁ будут равны δ _b = 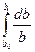= lnи

δ _l = . Относительные деформации δ _h, δ _b и δ _l называют истинными (логарифмическими, интегральными) деформациями. Отношения размеров тела после деформации к соответствующим размерам до деформации называют коэффициентами деформации. Для рассмотренного примера осадки параллелепипеда коэффициенты деформации следующие: η = 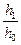- коэффициент обжатия; β = - коэффициент уширения; λ = - коэффициент вытяжки. Из условия постоянства объема металла при ОМД (5.1) получаем η β λ = 1, т. е. произведение коэффициентов деформации равно единице и после логарифмировния этого выражения получаем ln η + ln β + ln λ = 0, т. е. сумма истинных деформаций равна нулю. Отсюда следует, что истинные деформации не могут быть одного знака.

В инженерных расчетах некоторых процессов ОМД истинные деформации δ заменяют относительными ε, например, применительно к осадке и продольной прокатке соотношение между истинными и относительными деформациями определяется так:

δ _h = ln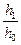= ln= ln (1+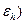; δ _b = ln= ln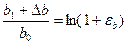

δ _l = .

Расхождение 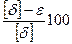% между истинными δ и относительными ε деформациями, например, для осадки при изменении последних в пределах 0,15—0,20 (5—20%) составляет 2—10,3%. Истинные деформации больше относительных. В инженерных расчетах при относительных деформациях меньше 0,1 принимают δ ≈ ε.

Истинные деформации обладают свойством аддитивности, т. е. их можно складывать при определении суммарной деформации, осуществленной за несколько операций.

В расчетах при обработке металлов давлением применяют различные величины, характеризующие деформацию: абсолютные, относительные и истинные деформации, а также коэффициенты деформации. Выбор характеристики деформации определяется удобствами вычисления и требуемой точностью расчета; правильнее определять истинную (лога­рифмическую) деформацию, которая удовлетворяет закону постоянства объема.

2.5 Механические схемы деформаций и напряжений в процессах ОМД. С. И. Губкин ввел понятие о схеме деформаций. Схемой деформаций называют графическое представление о наличии и знаке главных деформаций. Из условия постоянства объема при пластической деформа­ции следует, что главные деформации не могут быть одного знака, а схемы деформации могут быть только разноименные. Поэтому не может быть линейных схем деформации; имеются только одна плоская D ₁₁ и две объемных D ₁ и D ₁₁₁ схемы (рис.2.2). Схемы деформации графически представляют схему девиатора напряжений.

Рис. 2.2 Схемы деформации.

Дата добавления: 2014-01-04