Идеальный гармонический осциллятор. Уравнение идеального осциллятора и его решение. Амплитуда, частота и фаза колебаний

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Лекция 1

КОЛЕБАНИЯ

КОЛЕБАНИЯ. ВОЛНЫ. ОПТИКА

Колебание – один из самых распространённых процессов в природе и технике. Колебания – это процессы, повторяющиеся во времени. Колеблются высотные здания и высоковольтные провода под действием ветра, маятник заведённых часов и автомобиль на рессорах во время движения, уровень реки в течение года и температура человеческого тела при болезни. Звук – это колебания давления воздуха, радиоволны – периодические изменения напряжённости электрического и магнитного поля, свет – это тоже электромагнитные колебания. Землетрясения – колебания почвы, приливы и отливы – изменение уровней морей и океанов, вызываемые притяжением луны и т.д.

Колебания бывают механические, электромагнитные, химические, термодинамические и др. Несмотря на такое многообразие, все колебания описываются одними и теми же дифференциальными уравнениями.

Первыми учёными, изучавшими колебания, были Галилео Галилей и Христиан Гюйгенс. Галилей установил независимость периода колебаний от амплитуды. Гюйгенс изобрёл часы с маятником.

Любая система, которая, будучи слегка выведена из положения равновесия, совершает устойчивые колебания, называется гармоническим осциллятором. В классической физике такими системами являются математический маятник в пределах малых углов отклонения, груз в пределах малых амплитуд колебаний, электрический контур, состоящий из линейных элементов ёмкости и индуктивности.

Гармонический осциллятор можно считать линейным, если смещение от положения равновесия прямо пропорционально возмущающей силе. Частота колебаний гармонического осциллятора не зависит от амплитуды. Для осциллятора выполняется принцип суперпозиции - если действуют несколько возмущающих сил, то эффект их суммарного действия может быть получен как результат сложения эффектов от действующих сил в отдельности.

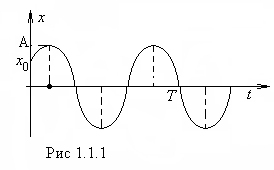Гармонические колебания описываются уравнением (рис.1.1.1)

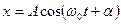(1.1.1)

где х -смещение колеблющейся величины от положения равновесия, А – амплитуда колебаний, равная величине максимального смещения, 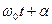- фаза колебаний, определяющая смещение в момент времени 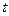, 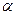- начальная фаза, определяющая величину смещения 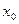в начальный момент времени, 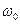- циклическая частота колебаний.

Время одного полного колебания называется периодом, , где 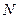- число колебаний, совершенных за время .

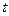Частота колебаний 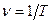определяет число колебаний, совершаемых в единицу времени, она связана с циклической частотой соотношением , тогда период .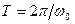

Скорость колеблющейся материальной точки

,

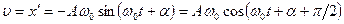ускорение

. (1.1.2)

Таким образом, скорость и ускорение гармонического осциллятора также изменяются по гармоническому закону с амплитудам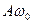и и соответственно. При этом скорость опережает по фазе смещение на , а ускорение – на (рис.1.1.2).

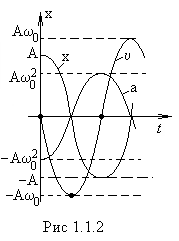Из сопоставления уравнений движения гармонического осциллятора (1.1.1) и (1.1.2) следует, что 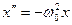, или

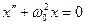. (1.1.3)

Это дифференциальное уравнение второго порядка называется уравнением гармонического осциллятора. Его решение содержит два постоянные а и 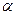, которые определяются заданием начальных условий

.

Отсюда .

Если периодически повторяющийся процесс описывается уравнениями, не совпадающими с (1.1.1), он н6азывается ангармоническим. Система, совершающая ангармонические колебания, называется ангармоническим осциллятором.

1.1.2. Свободные колебания систем с одной степенью свободы. Комплексная форма представления гармонических колебаний

В природе очень распространены малые колебания, которые система совершает вблизи своего положения равновесия. Если система, выведенная из положения равновесия, предоставлена себе, то есть на неё не действуют внешние силы, то такая система будет совершать свободные незатухающие колебания. Рассмотрим систему с одной степенью свободы.

Устойчивому равновесию соответствует такое положение системы, в котором её потенциальная энергия 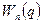имеет минимум (q – обобщённая координата системы). Отклонение системы от положения равновесия приводит к возникновению силы , которая стремится вернуть систему обратно. Значение обобщённой координаты, соответствующей положению равновесия, обозначим , тогда отклонение от положения равновесия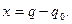

Будем отсчитывать потенциальную энергию от минимального значения . Примем 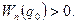Полученную функцию 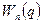разложим в ряд Маклорена и оставим первый член разложения, имеем: о

,

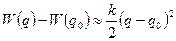где 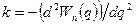. Тогда с учётом введённых обозначений:

, (1.1.4)

С учётом выражения (1.1.4) для силы, действующей на систему, получаем:

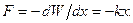
Согласно второму закону Ньютона, уравнение движения системы имеет вид: ,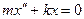

тогда

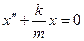, (1.1.5)

Выражений (1.1.5) совпадает с уравнением (1.1.3) свободных гармонических колебаний при условии, что

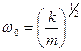, (1.1.6)

и имеет два независимых решения: 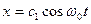и 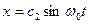, так что общее решение:

, или

,

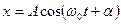где

Из формулы (1.1.6) следует, что частота определяется только собственными свойствами механической системы и не зависит от амплитуды и от начальных условий движения.

Зависимость координаты колеблющейся системы от времени можно определить в виде вещественной части комплексного выражения 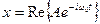, где A=Xe-iα – комплексная амплитуда, её модуль совпадает с обычной амплитудой, а аргумент – с начальной фазой.

1.1.3. Примеры колебательных движений различной физической природы

Дата добавления: 2014-01-04