Свободные затухающие колебания осциллятора с потерями

В любой реальной системе действуют силы трения, поэтому свободные гармонические колебания будут затухать. Затухающие колебания описываются уравнением:

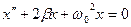(1.3.1)

где , r – коэффициент сопротивления, k – коэффициент упругости, β – коэффициент затухания, 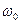– частота, с которой колебания совершались бы в отсутствии трения (собственная частота системы). Решение этого уравнения имеет вид:

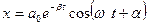, (1.3.2)

где α, 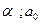- постоянные. Из (1.3.2) следует, что движение системы можно рассматривать как гармоническое колебание с амплитудой, меняющейся со временем по закону 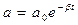(рис.1.3.1).

Скорость затухания колебаний определяется коэффициентом затухания β. Пусть τ – время, за которое амплитуда уменьшается в е раз. Тогда 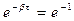и 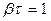, т.е. коэффициент затухания - это величина, обратная промежутку времени, за который амплитуда колебаний уменьшается в е раз.

Период колебаний: . Отношение амплитуд в двух соседних периодах называется декрементом затухания: .

Для характеристики колебательной системы используют логарифмический декремент затухания 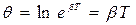. Тогда закон убывания амплитуды принимает вид 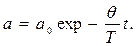За время τ амплитуда уменьшается в е раз, и система успевает совершить 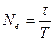колебаний. Имеем 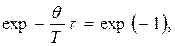и Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за время, в течение которого амплитуда уменьшается в е раз.

Время τ, за которое амплитуда уменьшается в е раз, называется временем релаксации колебаний.

Другой характеристикой колебательной системы является добротность

.

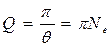Она пропорциональна числу колебаний 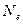за время релаксации.

Энергия системы пропорциональна квадрату амплитуды и при затухающих колебаниях убывает по закону

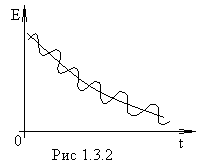
где - энергия колебаний в начальный момент времени (рис.1.3.2). Продифференцировав это выражение по времени, получим скорость убывания энергии 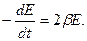Если изменение энергии за период мало, убыль энергии равн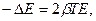а тогда

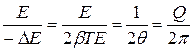
- при слабом затухании добротность пропорциональна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний. Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

С ростом коэффициента затухания период увеличивается, и при период колебаний обращается в бесконечность, т.е. движение перестает быть гармоническим.

Дата добавления: 2014-01-04