Резонанс в последовательном контуре

Вынужденные электрические колебания.

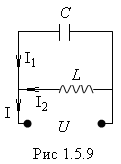
Чтобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний это можно осуществить, если включить последовательно с элементами контура переменную ЭДС или подать на контур переменное напряжение (рис.1.5.5).

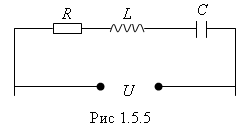Цепь, в которой последовательно с ЭДС включены сопротивление R, индуктивность L и конденсатор С, называется последовательным колебательным контуром. Рассмотрим процессы в этом контуре.

По второму правилу Кирхгофа 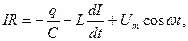или . Разделив на L, получаем уравнение вынужденных колебаний

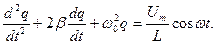(1.5.2)

Частное решение этого уравнения

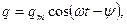(1.5.3)

где Подставим 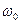и :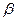

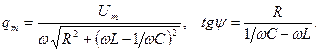
Общее решение получится, если к частному решению (1.5.3) прибавить общее решение однородного дифференциального уравнения, которое было получено в предыдущем параграфе. Оно содержит множитель , который очень быстро убывает, и при прошествии достаточно большого времени 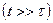им можно пренебречь. Таким образом, установившиеся вынужденные электромагнитные колебания в контуре описываются уравнением (1.5.3).

Силу тока в контуре при установившихся колебаниях найдем, продифференцировав (1.5.3) по времени:

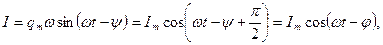
где 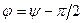- сдвиг фаз между током и приложенным напряжением. Тогда

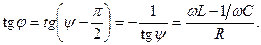
Из этого выражения следует, что ток отстает по фазе от напряжения (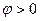)при 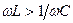. И опережает напряжение (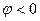) при 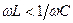. Для силы тока можно записать

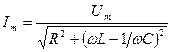. (1.5.4)

Представим соотношение (1.5.2) в виде: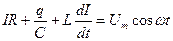. Произведение 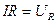- падение напряжения на активном сопротивлении; 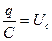- падение напряжения на конденсаторе; 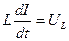– напряжение на индуктивности; тогда можно записать

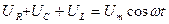. (1.5.5)

Таким образом, сумма напряжений на отдельных участках контура равна в каждый момент времени напряжению, приложенному извне.

Согласно (1.5.4) 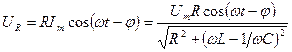- напряжение на активном сопротивлении совпадает по фазе с током в контуре.

Для напряжения на конденсаторе, подставив (1.5.3), имеем 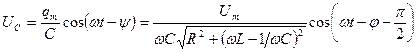– напряжение на ёмкости отстаёт от силы тока на π /2.

Напряжение на индуктивности 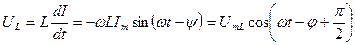, где 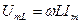,– напряжение на индуктивности опережает ток на π /2.

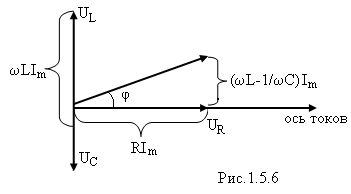
Фазовые соотношения можно представить наглядно с помощью векторной диаграммы. Действительно, гармонические колебания можно задать с помощью вектора, длина которого равна амплитуде колебаний, а направление вектора образует с некоторой осью угол, равный начальной фазе колебаний. Возьмём в качестве прямой, от которой отсчитывается начальная фаза, ось токов (рис. 1.5.6).

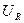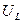совпадает по фазе с током, – отстаёт на π /2), – опережает на π /2. Векторы , , 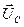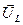в сумме дают 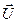, причём U определяется выражением (1.5.5).

При определенной частоте внешнего воздействия в контуре наступает резонанс. Резонансная частота для напряжения на конденсаторе и для заряда q равна:

Резонансные кривые для имеют вид, представленный на рис.1.5.7.

Все резонансные частоты . При ω→0 резонансные кривые сходятся в одной точке 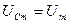– это напряжение на конденсаторе при подключении его к источнику постоянного напряжения 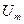. Максимум при резонансе тем острее и выше, чем меньше затухание β=R /2 L, то есть чем меньше R и больше L. Ход резонансной кривой аналогичен резонансной кривой при механических колебаниях.

Резонансные кривые для тока приведены на рис.1.5.8.

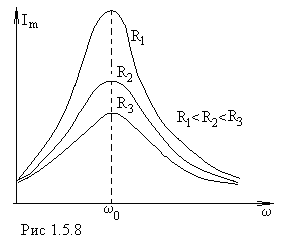
Амплитуда силы тока имеет максимальные значения, когда 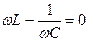, то есть резонансная частота для силы тока совпадает с собственной частотой колебаний контура:

При ω →0 сила тока уменьшается до нуля, так как при постоянном напряжении установившийся ток в цепи с конденсатором течь не может.

При малом затухании (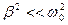) резонансную частоту для напряжения можно считать равной . Тогда отношение амплитуды напряжения на конденсаторе при резонансе к амплитуде внешнего напряжения равно:

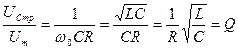
- то есть добротность контура показывает, во сколько раз напряжение на конденсаторе может превышать приложенное напряжение.

Итак, при резонансе 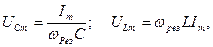причём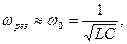

поэтому 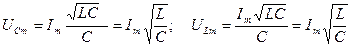- амплитуды напряжений на ёмкости и индуктивности равны между собой, но противоположны по фазе. Поэтому напряжения на ёмкости и индуктивности компенсируют друг друга, и цепь ведёт себя цепь только с активным сопротивлением. Вся энергия, приложенная к контуру, идёт на Ленц-Джоулево тепло. Ток в цепи достигает максимального значения. Это резонанс напряжений – индуктивного 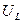и емкостного .

Дата добавления: 2014-01-04