Импульс электромагнитного поля. Закон сохранения импульса и момента импульса

Просуммируем все уравнения движения частиц, находящихся в поле, в выражении (2.36)

.

Будем считать распределение зарядов в пространстве непрерывным, поэтому сумму заменим интегралом по объему системы:

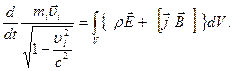(2.45)

Подставим значения 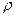и из уравнений Максвелла:

. (2.46)

Чтобы в правой части этого равенства получить производную по времени, дополним его слагаемым . Это равенство всегда равно нулю, так как , т.е. 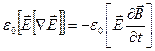, тогда

Таким образом, равенство (2.46) не нарушается. Кроме того, добавим еще . Очевидно, 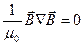, так как 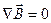. Получаем:

Сгруппируем:

Подставив в выражение (2.45), получаем

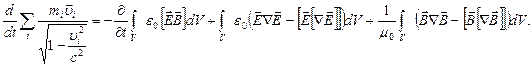
В случае изолированной системы поле-заряды второй и третий интегралы можно свести к поверхностным, и при интегрировании по всему пространству они дают 0. В результате имеем

,

или

(2.47)

- это закон сохранения импульса для изолированной системы поле-заряды.

Величина

(2.48)

есть плотность импульса.

Выражение (2.47) можно сформулировать так: в изолированной системе поле-заряды полный импульс, равный релятивистскому импульсу заряженных частиц и импульсу электромагнитного поля, сохраняется.

Из выражения (2.48) следует, что плотность импульса отлична от нуля только в том случае, если существуют оба поля и , непараллельные друг другу.

Взаимодействие между заряженными телами осуществляется посредством поля. Это приводит к несохранению импульса замкнутой механической системы материальных точек, если система обменивается импульсом с полем так, что импульс поля изменяется. В такой системе может не выполняться третий закон Ньютона. Например, излучающее, рассеивающее, отражающее или поглощающее электромагнитные волны тело испытывает со стороны поля действие силы, т.к. импульс тела меняется, но эта сила не имеет противодействующей – к полю не может быть приложена сила.

Обладая импульсом, электромагнитное поле оказывает давление на тела, с которыми взаимодействует. Примером тому – световое давление.

Плотность момента импульса электромагнитного поля найдем по правилу, известному из механики:

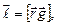
где - радиус-вектор точки, в которой определяются и 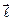. Умножая (2.47) векторно справа на , получаем закон сохранения момента импульса в изолированной системе поле-заряды:

.

Из (2.47) следует, что .

Дата добавления: 2014-01-04