Математическое дисконтирование по простым процентам

В финансовой практике часто приходится решать задачу, обратную вычислению наращенной суммы, которая может быть сформулирована таким образом: определить сумму 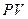, которую необходимо инвестировать в данный момент времени, с тем, чтобы через некоторый определенный период 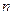получить при установленной ставке процента 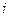требуемую наращенную сумму 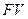. Для решения этой задачи применяется операция дисконтирования.

Дисконтирование позволяет по известным наращенной сумме, процентной ставке и сроке финансовой операции определить современную стоимость этой наращенной суммы.

Другими словами дисконтирование позволяет определить, какую первоначальную сумму надо дать в долг, чтобы получить в конце срока сумму 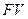при условии, что на долг начисляются проценты по ставке .

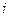В зависимости от вида процентной ставки применяются два вида дисконтирования: математическое дисконтирование и банковский (коммерческий) учет. В первом случае при расчете применяют обычные (декурсивные), а во втором – авансовые проценты.

Рассмотрим, как производится математическое дисконтирование.

Выразив из формулы (2.1) 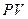, получим формулу математического дисконтирования:

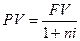, (2.5)

Здесь 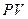- современная стоимость наращенной (будущей) суммы денег 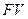; 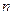- срок проведения финансовой операции (число процентных периодов); 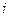- процентная ставка.

Дисконтный множитель 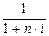показывает, какую долю составляет первоначальная величина долга 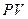в его окончательной сумме .

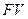Пример. Заемщик должен возвратить кредит единовременным платежом с процентами за период 2 года. Проценты по кредиту составили 12% годовых. Какую сумму получил заемщик в момент заключения кредитного договора и чему равен дисконт, если сумма к возврату составляет 1 500 000 рублей?

Решение: FV=1500 000 рублей; n=2 года; i= 0,12

,

.

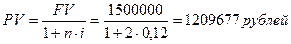В случае если срок финансовой операции задан в днях или в месяцах, из формулы (2.2) получим формулу математического дисконтирования для 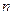<1:

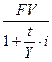, ( 2.6 )

где - длительность финансовой операции в днях (в месяцах); 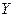- число дней (месяцев в году).

Пример. Какую сумму инвестор должен внести сегодня под 16% годовых, чтобы через 180 дней после подписания договора накопить 310 тыс. руб. при условии, что начисляются простые точные проценты.

n Решение: FV=310 000 рублей; t=180 дней; i=0,16; Y=365 дней.

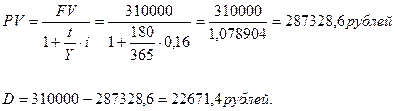
Дата добавления: 2014-01-04