Представление о квантовой механике

Окружающий нас макромир описывается классической механикой Ньютона, а микромир – мир мельчайших частиц (электронов, протонов, нейтронов, ядер, атомов и молекул) – своей механикой, названной волновой или квантовой механикой. Эти термины отражают главные отличия микромира от макромира: дискретность значений физических величин (квантование) и активное проявление волновых свойств.

Уравнения Ньютона описывают макромир, микромир описывает уравнение Шредингера, являющееся дифференциальным уравнением второго порядка; для неизменного во времени состояния одной частицей массы m оно имеет вид:

, (1.16)

где ψ – переменная величина, так называемая волновая функция, смысл которой будет ясен ниже; U – потенциальная энергия частицы; Е – полная энергия частицы.

Полностью это уравнение решается лишь для атома водорода, водородоподобных частиц и молекулярного иона Н₂^Å. Для остальных частиц (многоэлектронных атомов и молекул) уравнение Шредингера может быть решено лишь приблизительно. Решение уравнения (1.16) для атома водорода и водородоподобных частиц, выводы и следствия, вытекающие из этого решения, составляют предмет квантовой механики. Подходы и методы решения уравнения Шредингера для многоэлектронных систем составляют предмет квантовой химии.

Микромир существенно не похож на наш мир, это мир вероятностных представлений, где нельзя точно указать, где находится в настоящий момент та или иная частица, а можно лишь вычислить вероятность её нахождения в той или иной области или точке пространстве. В микромире не говорят о движении, а говорят о состоянии частиц, в частности электронов. Состояние каждой частицы в микромире описывается специальной функцией (ψ-функцией), называемой волновой функцией. Это своеобразный собирательный образ волнового мира; любая задача в микромире сводится к нахождению волновой функции. Величина этой функции пропорциональна значению амплитуды волны де Бройля для данной частицы. Квадрат значения волновой функции частицы в данной точке пространства равен вероятности нахождения этой частицы в этой точке пространства. Произведение квадрата волновой функции частицы на объём передаёт вероятность нахождения данной частицы в этом объёме. Традиционно пространство вокруг ядра, в котором наиболее вероятно нахождение электрона, называют орбиталью; а в целом, электроны, двигаясь вокруг ядра, образуют электронное облако.

Микромир разительно отличается от нашего макромира, он живёт по своим законам, зачастую не имеющим аналогов в макромире и представляющимся порой абсурдными. Поэтому не следует все представления микромира пытаться представить или, наоборот, образы и понятия нашего мира перенести в мир микрочастиц. Приведём один характерный пример. В микромире, описываемом квантовой механикой, нет понятия «размер», совершенно естественного в окружающем нас мире. Тем не менее, попытаемся перенести из макромира в микромир это понятие. Единственной величиной в волновом мире, которой можно приписать смысл понятия «размер», является длина волны. Пусть микрочастица массой m движется со скоростью V. Длина волны де Бройля для неё составит:

Разрезаем эту частицу пополам, не изменяя скорости. Для половинок, имеющих массу m/2, длина волны де Бройля составит:

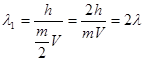
Иными словами половинка частицы оказалась в два раза больше, чем целая частица. Этот абсурдный вывод мы получили лишь потому, что для микромира использовали чуждое ему понятие.

Волновые свойства для объектов окружающего нас мира не проявляются в силу мизерного значения постоянной Планка, они должны быть характерны для объектов размером порядка нанометров (1 нм = 1·10^–9 м = 1·10^–7 см). Совсем недавно учёные и инженеры научились уверенно получать материалы с подобной степенью диспергирования вещества. Они так и называются «наноматериалы» и уже появилось технологическое направление – нанотехнология. Специалистов этого профиля будут готовить в РХТУ им. Д.И. Менделеева.

Дата добавления: 2014-01-04