Задачи и упражнения. Пример 1. Найти длину волны излучения, соответствующую второй линии серии Бальмера спектра испускания атомарного водорода

Пример 1. Найти длину волны излучения, соответствующую второй линии серии Бальмера спектра испускания атомарного водорода.

Решение. Воспользуемся формулой Ридберга (1.1) для спектра испускания атомарного водорода

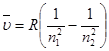
Для второй линии серии Бальмера n₁=2, n₂= 4, следовательно

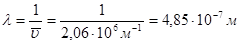
Пример 2. Найти длинноволновую и коротковолновую границы второй серии линий в спектре испускания водородоподобного иона гелия.

Решение. Водородоподобный ион гелия – это ион Не⁺; заряд ядра равен 2; второй серии соответствует n₁=2. Коротковолновой границе отвечает самая маленькая длина волны (самое большое волновое число); этому соответствует n₂= ∞; получаем из соотношения (1.3):

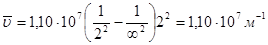
Длинноволновой границе отвечает самая большая длина волны (самое маленькое волновое число); этому соответствует n₂=3; получаем:

Пример 3. Определить энергию кванта излучения, соответствующего третьей линии второй серии (серии Бальмера) в спектре испускания атома водорода.

Решение. Энергия кванта излучения определяется соотношением (1.4):

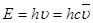
Для серии Бальмера n₁=2, третьей линии соответствует n₂=5. Находим по соотношению (1.1):

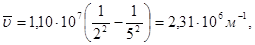
а затем – энергию кванта:

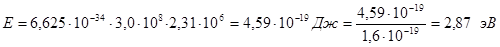
Пример 4. Вычислить скорость электрона на первой боровской орбите в атоме водорода.

Решение. Согласно соотношению (1.10):

; z=1; n=1

Подставляем константы в это уравнение, помня, что его выводили в системе СГС:

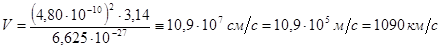
Таким образом, скорость электрона в атоме водорода составляет около одной трёхсотой части от скорости света.

Пример 5. Охарактеризовать квантовыми числами все электроны атома азота в основном состоянии.

Решение. Атом азота содержит 7 электронов. Учёт принципа Паули и правила Хунда приведёт к следующему распределению электронов:

№ п/п	n	ℓ	mℓ	ms
				+1/2
				–1/2
				+1/2
				–1/2
				+1/2
				+1/2
			–1	+1/2

Поскольку энергия электрона не зависит от магнитного квантового числа, то порядок выхода значений m_ℓ для ℓ=1 (р-оболочка) любой.

Пример 6. Охарактеризовать квантовыми числами электроны следующего состояния

Решение. Все указанные электроны имеют n=6 и ℓ=2; у пяти электронов m_s = +1/2, а у остальных m_s = –1/2. Поскольку энергия электрона не зависит от m_ℓ, то парные электроны с m_s = –1/2 могут находиться в любой паре квантовых ячеек. Иными словами, электроны с m_s = –1/2 могут иметь любые два значения m_ℓ из пяти разрешенных.

№ п/п	n	ℓ	Mℓ	ms
				+1/2
			–2	+1/2
				+1/2
				+1/2
			–1	+1/2
				–1/2
				–1/2

Точно так же безразличен порядок выхода значений m_ℓ для первых пяти электронов, имеющих m_s = +1/2.

Пример 7. Охарактеризовать квантовыми числами 3d-электроны атома хрома в основном состоянии.

Решение. Электронная формула атома хрома: KL 3s²3p⁶3d⁵4s¹ (провал электрона!). Следовательно, 3d-электроны будут распределены следующим образом

№ п/п	n	ℓ	mℓ	ms
				+1/2
			–2	+1/2
				+1/2
			–1	+1/2
				+1/2

Еще раз обратим внимание, что порядок выхода значений m_ℓ может быть любой из массива разрешённых значений.

Дата добавления: 2014-01-04