Линейные регрессионные модели

Постановка задачи:

Пусть есть статистические данные по изучаемым величинам, n наблюдений.

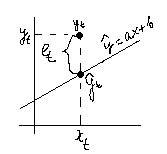
В системе (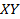) отметим эмпирические точки ()

…	…

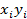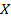
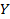
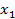
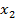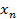
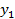
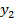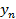
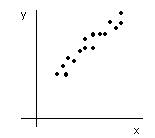
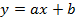
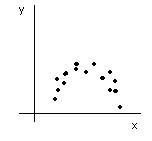
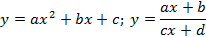
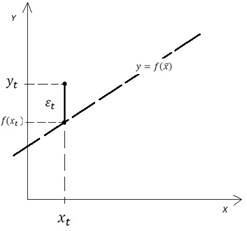
По расположению точек или из теории определяется класс функций.

Предположим, что зависимость линейная 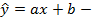наилучшая линия.

Рассмотрим функционалы:

;

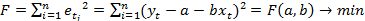
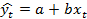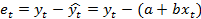
Метод нахождения коэффициентов уравнения модели, основанный на минимизации суммы квадратов отклонений, называется метод наименьших квадратов (МНК). Уравнение, полученное по МНК, называется уравнением линии регрессии.

Необходимые условия (в данном случае и достаточные):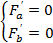

КЛАССИЧЕСКАЯ РЕГРЕССИОННАЯ МОДЕЛЬ (КРМ)

Определение: Линия регрессии. Каждому 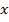ставится в соответствие математическое ожидание 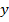при условии, что 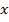принимает свое конкретное значение. Тогда регрессия называется линейной.

Чаще в природе встречается нормальное распределение.

КРМ

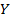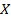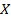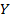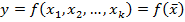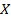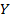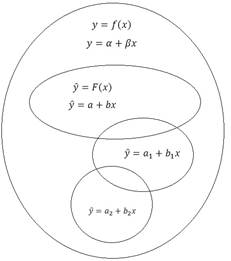
Генеральная совокупность. Есть и некоторый набор случайных величин . Между и объективно существует некоторая зависимость, т.е. уравнение отражает идеальную зависимость между величинами и во всей генеральной совокупности при прочих равных условиях. По результатам наблюдения и применяя МНК, строим уравнение линии регресси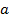и.

и 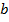– оценки для коэффициентов 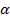и .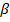

Условия классической регрессии:

У1. Между 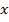и 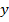существует зависимость.

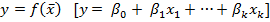
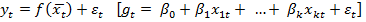
При этом 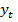и 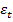- случайные величины и их 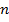штук.

У2. Факторные переменные 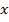детерминированы (не являются случайными), наблюдаются без ошибок, и столбцы со значением факторных переменных вместе со столбцами значением «1» линейно независимы. Т.е. матрица

			…
			…
			…
…	…	…	…	…
			…

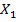
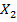
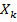
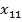
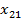
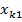
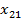
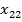
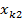
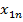
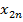
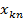
имеет максимальный ранг.

У3. Математическое ожидание ошибки равно нулю 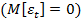, т.е. ошибки не имеют систематической составляющей.

У4. Дисперсия ошибки 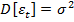постоянна, не зависит от номера наблюдения.

У5. Ошибки 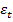между собой статистически не зависимы между собой: .

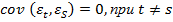Замечание: из У4 и У5 следует: ковариация матриц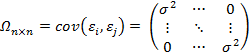

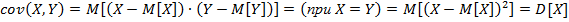
Или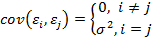

Замечание: если У4 и У5 выполнены, то говорят, что модель гомоскедастична. Проиллюстрируем:

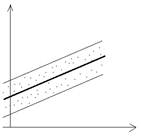
У6. Ошибки 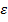и фактические переменные 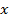статистически независимы.

У7*. Ошибки подчиняются нормальному закону распределения с 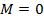и . .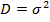

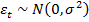Дата добавления: 2014-01-04