Циклические коды

Был предложен ряд кодов и способов декодирования, при которых сложность декодера растет не экспоненциально, а лишь как некоторая степень n. В классе линейных систематических двоичных кодов это - циклические коды. Циклические коды просты в реализации и при невысокой избыточности обладают хорошими свойствами обнаружения ошибок. Циклические коды получили очень широкое распространение как в технике связи, так и в компьютерных средствах хранения информации. В зарубежных источниках циклические коды обычно называют избыточной циклической проверкой (CRC, Cyclic Redundancy Check).

Рассмотрим данный класс кодов подробнее. Название циклических кодов связано с тем, что каждая кодовая комбинация, получаемая путем циклической перестановки символов, также принадлежит коду. Так, например, циклические перестановки комбинации 1000101 будут также кодовыми комбинациями 0001011, 0010110, 0101100 и т.д.

Представление кодовых комбинаций в виде многочленов F(x) позволяет установить однозначное соответствие между ними и свести действия над комбинациями к действию над многочленами. Сложение двоичных многочленов сводится к сложению по модулю 2 коэффициентов при равных степенях переменной x. Умножение производится по обычному правилу умножения степенных функций, однако полученные коэффициенты при данной степени складываются по модулю 2. Деление осуществляется, как обычное деление многочленов, при этом операция вычитания заменяется операцией сложения по модулю 2. Циклическая перестановка кодовой комбинации эквивалентна умножению полинома F(x) на x с заменой на единицу переменной со степенью, превышающую степень полинома.

Любой полином G(x) степени r<n, который делит без остатка двучлен xⁿ - 1, может быть порождающим полиномом циклического (n,k)-кода, где k = n - r. В этот код входят те полиномы, которые без остатка делятся на G(x).

Особую роль в теории циклических кодов играют неприводимые многочлены G(x), т.е. полиномы, которые не могут быть представлены в виде произведения многочленов низших степеней.

Идея построения циклического кода (n,k) сводится к тому, что полином Q(x), представляющий информационную часть кодовой комбинации, нужно преобразовать в полином F(x) степени не более n -1, который без остатка делится на порождающий полином G(x) (неприводимый многочлен) степени r = n - k. Рассмотрим последовательность операций построения циклического кода.

· Представляем информационную часть кодовой комбинации длиной k в виде полинома Q(x).

· Умножаем Q(x) на одночлен x^rи получаем Q(x)x^r.

· Делим полином Q(x)x^r на порождающий полином G(x) степени r, при этом получаем частное от деления C(x) такой же степени, что и Q(x).

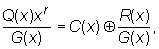где R(x) - остаток от деления Q(x)x^r на G(x).

Умножив обе части на G(x), получим .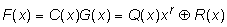

Полином F(x) делится без остатка на G(x), т.е. представляет собой разрешенную комбинацию циклического (n,k)-кода.

Таким образом, разрешенную кодовую комбинацию циклического кода можно получить двумя способами: умножением кодовой комбинации простого кода C(x) на полином G(x) или умножением кодовой комбинации Q(x) простого кода на одночлен x^r и добавлением к этому произведению остатка R(x).

В первом случае информационные и проверочные разряды не отделены друг от друга (код получается неразделимым). Во втором случае получается разделимый код. Этот код достаточно широко используется на практике, поскольку процесс декодирования и обнаружения ошибок при использовании разделимого кода выполняется проще.

Рассмотрим пример разделяемого циклического кода (9,5) с порождающим полиномом 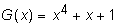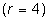. В качестве информационной части кодовой комбинации возьмем полином .

Умножение Q(x) на x^r эквивалентно повышению степени многочлена на r. Q(x) = 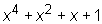® 10111.

Q(x)x^r = 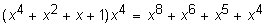® 101110000

Формирование проверочной группы осуществляется в процессе деления Q(x)x^r на G(x).

В результате деления получаем частное от деления C(x) = x⁴+x² ® 10100 и остаток от деления R(x) = x³+x² ® 1100. Для получения разрешенной кодовой комбинации остаток (проверочная группа) помещается на место "пустых" разрядов Q(x)x^r, т.е. F(x)= 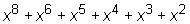® 101111100. Данная комбинация отправляется в канал связи. Аналогичные операции выполняются для других информационных комбинаций.

Обнаружение ошибок при циклическом кодировании сводится к делению принятой кодовой комбинации на тот же образующий полином, который использовался для кодирования. Если ошибок в принятой комбинации нет (или они такие, что передаваемую комбинацию превращают в другую разрешенную), то деление на образующий полином производится без остатка. Наличие остатка свидетельствует о присутствии ошибок.

При использовании в циклических кодах декодирования с исправлением ошибок остаток от деления может играть роль синдрома. Нулевой синдром указывает на то, что принятая комбинация является разрешенной. Всякому ненулевому синдрому соответствует определенная конфигурация ошибок, которая и исправляется.

Однако, обычно в системах связи исправление ошибок при использовании циклических кодов не производится, а при обнаружении ошибок выдается запрос на повтор испорченной ошибками комбинации. Такие системы называются системами с обратной связью и будут рассмотрены ниже в подразделе 6.1.2.8.

Дата добавления: 2014-01-04