Построение системы уравнений Колмогорова на основе графа состояний системы

Обозначим через вероятность нахождения технической системы в i -ом состоянии в момент времени t, 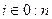. Эти вероятности удовлетворяют системе дифференциальных уравнений Колмогорова. Рассмотрим как её построить.:

· Вероятность, что система перейдет из состояния j в состояние i при условии, что в t она находится в состоянии j, равна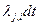

· Вероятность, что система перейдет из состояния i в состояние j при условии, что в t она находится в состоянии i, равна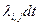

· Вероятность, что система не перейдет из состояния i в другое состояние при условии, что в t она находится в состоянии i, равна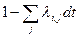

·

Тогда вероятность того, что система окажется в состоянии i в момент времени t+dt определяется как:

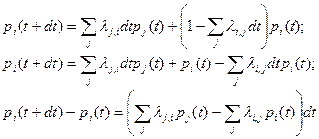
(1)

Данная система уравнений составляется по следующему правилу:

1. для каждого состояния 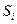записывается уравнение;
2. в левой части уравнения стоит производная от ;
3. в правой части уравнения стоит сумма следующих слагаемых:
1. если возможен переход из состояния j в состояние i, то слагаемое будет равняться произведению вероятности состояния j на интенсивность перехода из j в i: ;
2. если возможен переход из состояния i в состояние j, то слагаемое будет равняться произведению вероятности состояния i на интенсивность перехода из i в j со знаком минус:

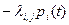
Рассмотрим это на примере дублированной восстанавливаемой системы. Сначала построим для неё граф состояний. При этом будем полагать, что при восстановлении элемент 1 имеет приоритет над элементом 2.

Структурная схема

Граф состояний

Состояния:   0 – работает элемент 1, элемент 2 работоспособен 1 – работает элемент 2, элемент 1 не работоспособен и восстанавливается 2 – работает элемент 1, элемент 2 не работоспособен и восстанавливается 3 – оба элемента неработоспособны, восстанавливается только элемент 1

Теперь по графу состояний составим систему дифференциальных уравнений:

(2)

Проверить правильность составленной системы уравнений можно с помощью следующего выражения: .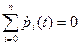

Чтобы получить частное решение этой системы необходимо знать начальные условия – вероятности нахождения систему в состояниях в начальный момент времени: 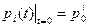. В рассматриваемом примере начальным является состояние с номером ноль, поэтому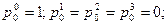

Систему уравнений (1) можно записать и в матричном виде. Введем следующие обозначения:

• - вектор вероятностей состояний;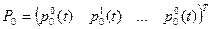
• - вектор начальных вероятностей состояний;
• - вектор производных вероятностей состояний;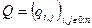
• - матрица интенсивностей.

Тогда 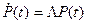(3)

Для нашего примера:

В матричном виде решение уравнения (3) представим с помощью матричной экспоненты: 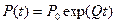. (4)

Для решения системы (1) можно применять различные методы. В том числе и метод преобразований Лапласа. Тогда система (1) запишется в виде системы алгебраических уравнений:

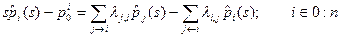
Для нашего примера:

Найдя изображение можно получить оригинал с помощью любого известного метода.

Если 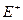- множество работоспособных состояний системы, а - множество неработоспособных состояний, то ввиду несовместности различных состояний функции готовности и простоя системы будут соответственно равны:

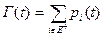(5)

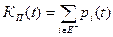(6)

В нашем примере ;.

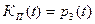Дата добавления: 2014-01-03