Уравнение Э.Шредингера. Квантовые числа

Теперь все резко усложняется, поскольку электрон размазан в атоме и его движение нужно описывать как волновое, приходится вводить так называемую волновую функцию y(x,y,z), описывающую движение электрона как волны. Чтобы описать положение электрона в атоме необходимо найти, хотя бы приблизительно, где можно обнаружить этот размазанный электрон, т.е. определить наиболее вероятный радиус орбиты, определить его энергию и т.о. описать спектры атомов.

Вероятность нахождения электрона в заданной точке пространства и его энергии описываются волновой функцией. Волновая функция для данного электрон также, называется орбитальной волновой функцией. Область пространства, где в данный момент электрон может находиться с достаточно высокой вероятностью, называется орбиталью.

Согласно определению В.И. Пупышева, орбиталь – функция декартовых координат электрона, т.е. вектора с координатами x,y,z, не имеющая самостоятельного физического смысла. Смысл имеет лишь y² (а если волновая функция комплексна, то квадрат ее модуля), определяющий вероятность найти электрон в данной области пространства.

В 1926г. Эрвин Шредингер предложил уравнение, получившее название волнового уравнения Шредингера.

, (3.9)

где U – потенциальная энергия электрона;

E – полная энергия электрона,

y сумма вторых производных волновой функции по осям координат x,y,z;

m – масса электрона,

h – постоянная Планка.

Это уравнение связывает волновую функцию y с потенциальной энергией электрона U и его полной энергией E,

Для описания положения и энергии электрона в атоме используется четыре квантовых числа. Эти числа можно рассматривать как некие коэффициенты в решениях важнейшего в квантовой механике уравнения Шредингера.

Главное квантовое число n эквивалентно квантовому числу в теории Бора. Оно в основном определяет энергию электронов на данной орбитали:

E_n =-(2p²me⁴Z²)/(n²h²) =-13,6 эВ*Z²/n²,

где Z – заряд ядра, допустимые значения n = 1(K), 2(L), 3(M), 4(N), 5(O)…

Орбитальное квантовое число l определяет значение орбитального момента количества движения электрона на данной орбитали (характеризует форму орбитали).

, (3.10)

допустимые значения l = 0, 1, 2, 3 …, n-1

Исторически первые четыре значения орбитального квантового числа l имеют буквенные символы, произошедшие от спектроскопических терминов, использованных в 1890-е годы при описании спектров щелочных металлов: 0 – s (sharp – резкий), 1 – p (principal – главный), 2 – d (diffuse – диффузный), 3 – f (fundamental – фундаментальный). Изображаемые в учебниках «формы» орбиталей представляют собой графики функций, изображающие области математического пространства, где нахождение электрона данной орбитали наиболее вероятно. Эта область определяется квадратом соответствующей волновой функции.

n=1	l=0	m=0	1s
n=2	l=0	m=0	2s
	l=1	m=-1,0,1	2px, 2py,2pz
n=3	l=0	m=0	3s
	l=1	m=-1,0,1	3px,3py,3pz
	l=2	m=±2,±1,0	3dxy,yz,xz,
n=4	l=0	m=0	4s
	l=1	m=-1,0,1	4px,4py,4pz
	l=2	m=±2,±1,0	4d
	l=3	m=±3, ±2, ±1,0	4f (7 орбиталей)

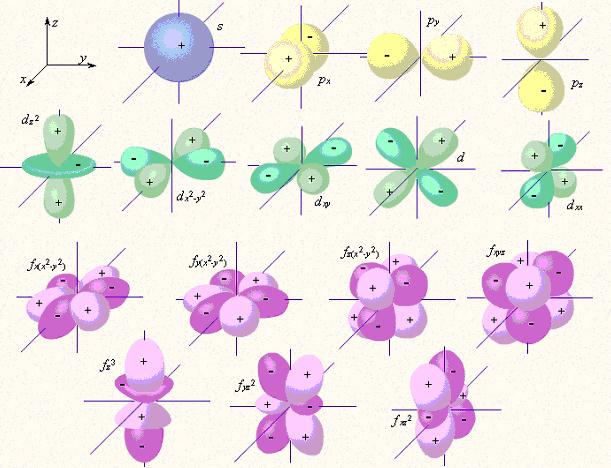
А вот так выглядят s,p,d-орбитали

Рисунок 3.6 -Изображение с помощью граничных поверхностей s-, p-, d- и f-орбиталей

Магнитное квантовое число m_l определяет значение составляющей проекции момента количества движения электрона на выделенное направление в пространстве: m_l (h/2p) (характеризует ориентацию орбиталей в пространстве). В отсутствие внешнего магнитного поля электроны на орбиталях с одинаковым значением орбитального квантового числа l энергетически равноценны (т.е. их энергетические уровни вырождены). Однако в постоянном магнитном поле некоторые спектральные линии расщепляются. Это означает, что электроны становятся энергетически неравноценными. Например, p-состояния в магнитном поле принимают 3 значения вместо одного, d-состояния – 5 значений. M_z = h*m_l/2p. Допустимые значения m_l для данного l: -l…,0,…+l

Спиновое квантовое число m_s связано с наличием собственного магнитного момента у электрона. В общем виде выражение для магнитного момента количества движения совпадает с таковым для орбитального момента: M_s = [m_s(m_s+1)]^1/2h/2p. Для электрона m_s принимает только два значения: +1/2 и -1/2. Иногда для более наглядного объяснения понятия спина используют грубую аналогию – электрон представляют как летящий волчок (круговой ток, создающий собственное магнитное поле). Такая аналогия позволяет объяснить наличие спина +1/2 у электрона и протона, но не у нейтрона – частицы с нулевым зарядом. Электроны с разными спинами обозначаются ­¯.

Понятие «спин» не укладывается в наши «макропредставления» о пространстве. При всех способах его регистрации спин всегда направлен вдоль той оси, которую наблюдатель выбрал за исходную. Значение спина 1/2 означает, что электрон (протон, нейтрон) становится идентичным сам себе при обороте на 720^о,а не 360^о, как в нашем трехмерном мире.

Рассмотренные выше квантовые числа могут показаться понятиями абстрактными и далекими от химии. Действительно, пользоваться ими для расчетов строения реальных атомов и молекул можно только при наличии специальной математической подготовки и мощной ЭВМ. Однако, если добавить к схематично изложенным понятиям квантовой механики еще один принцип, квантовые числа «оживают» для химиков.

И так, электрон в атоме характеризуется:

1. Главным квантовым числом n, указывающим на энергию электрона;

2. Орбитальным квантовым числом l, указывающим на характер орбиты;

3. Магнитным квантовым числом, характеризующим положение облаков в пространстве;

4. И спиновым квантовым числом, характеризующим веретенообразное движение электрона вокруг своей оси.

Дата добавления: 2014-01-04