
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закон Ньютона
|
|
|
|
Свойства
П. 2. Пространство
П. 1. Пространство.
Пространства суммируемых функций.
Произведение мер. Теорема Фубини.
П. 6. Сравнение интеграла Лебега с интегралом Римана
Пусть - классическая мера Лебега.
Теорема 10. Если, то - интегрируема по Лебегу на и
Разбиение на частей точками
Суммы Римана-Дарбу:
Пусть:
По Теореме Леви: и
почти всюду.
∎
Утверждения:
1) Если и несобственный интеграл, то
2) Если несобственный интеграл сходится абсолютно, то
3) Если несобственный интеграл сходится условно, то интеграл Лебега не существует.
Пример: - сходится условно, т.к. расходится
Пусть - полукольца.
- полукольцо.
- мера на, - аддитивная.
- мера на, - аддитивная.
Тогда - мера, - аддитивная.
- измеримо.
Теорема Фубини. Пусть, интегрируема по мере на, тогда
(без доказательства).
Пусть на задана мера - полная.
Разобьем множество функций на на классы эквивалентности на.
пространство суммируемых на функций, то есть
- линейное пространство.
Теорема. Пространство - полное.
Пусть - фундаментальная последовательность
Выберем сходится. по следствию из теоремы Леви - сходится почти всюду. сходится почти всюду.
Докажем, что
- фундаментальна
по теореме Фату, то есть ∎
Опр. Множество называется плотным в множестве, если любая окрестность любой точки из множества содержит точку из множества.
Например, плотно в.
в всюду плотно множество интегрируемых функций с конечным числом значений.
в всюду плотно множество интегрируемых непрерывных функций.
Опр. Мера называется мерой со счетным базисом, если счетная система измеримых множеств, такая что для измеримого
Пример: на отрезке счетным базис – множество промежутков с рациональным и концами (и их объединениями).
Опр. Пространство называется сепарабельным, если в нем существует счетное всюду плотное множество.
Если мера - мера со счетным базисом, то - сепарабельно.
Счетное всюду плотное множество:
- индикатор множества или характеристическая функция множества.
Счетное всюду плотное множество для
множество многочленов с рациональными коэффициентами
тригонометрическая система функций
- множество функций с интегрируемым квадратом, то есть
∎
- интегрируема ∎
- линейное пространство.
Неравенство Коши — Буняковского.
Неравенство Минковского.
- полное без доказательства. ∎
- сепарабельно. (для со счетным базисом).
Для счетное всюду плотное множество – ортогональная тригонометрическая система.
Для многочлены Эрмита.
в интеграле
F=mā
ā=F/m
F – равнодействующая сила, равна ∑всех сил.
| Свободные | Вынужденные | |||||||||
| незатухающие | затухающие | |||||||||
| Силы, действующие в системе, где совершаются колебания | ||||||||||
| F упр. | F упр., F тр. | F упр., F тр., F вн. | ||||||||
| Второй закон Ньютона | ||||||||||
| mв=F упр | mв=F упр+F тр | mв=F упр+F тр + F вн | ||||||||
| Вывод дифференциального уравнения колебания | ||||||||||
| ma=-kx ma+kx=0 ⃒:m a+kx/m=0 | ma=-kx-rV
ma+kx+rV= 0⃒:m
a+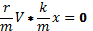
| ma=-kx-rV+ F max * sinщвнеш.t
ma+kx+rV= F max * sinщвнеш.t ⃒:m
a+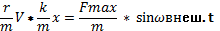
| ||||||||
| Дифференциальные уравнения колебаний | ||||||||||
| x”+ щ02x=0 | x” + 2вx` + щ02x=0 | x” + 2вx` + щ02x= F max * sinщвнеш.t | ||||||||
| Решение дифференциальных уравнений. Зависимость x(t) | ||||||||||
x= Asin(щ0t + 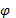 0) 0)
| x= A0 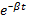 sin(щ03t + sin(щ03t + 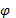 0) 0)
| x=Aвнеш*sin(Wвнеш*t+ц0) | ||||||||
| Частота, с которой совершается колебания | ||||||||||
щ0 – собственная циклическая частота
щ0 = 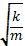
| щзатух. – частота затухающих колебаний
щзатух. = 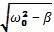
| щвнеш. – частота внешней периодической силы | ||||||||
| Зависимость амплитуды от времени | ||||||||||
A = const
 A, м A, м
t, c
| в2›в    1
A, м
A, c
2 1
0 t, c
A = A0 1
A, м
A, c
2 1
0 t, c
A = A0 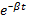
|      Авнеш=const Авнеш=const
| ||||||||
Пояснения к таблице:
Fтр= -rV
r – коэффициент трения
[r]=кг/с
V – скорость движения тела
[V]=м/с
Знак «-» показывает, что сила трения направлена против V движения тела.
Fвнеш – внешняя периодичекая сила
Fвнеш=Fmax*sinWвнеш*t
Fmax – max значение силы, амплитуда.
Wвнеш – частота внешней периодической силы
X – смещение тела от положения равновесия
V=X` – первая производная смещения тела по времени
ā – ускорение тела; [ā]=м/с2
ā=X` – вторая производная смещения тела по времени
k/m=W02; W0 – собственная циклическая частота; [W0]=рад/с
m*r/m=2β, β – коэффициент затухания; [β]=с-1
Fmax/m=ξmax
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 405; Нарушение авторских прав?; Мы поможем в написании вашей работы!

