Сложение отраженных волн. Стоячие волны

Условия минимума

Условия максимума

A_рез=2Acos*W∆r/2υ

W∆r/2υ=Ф

A_рез max если cosФ=1

W∆r/2υ=kπ

W=2π/T

υ=λ/T

2π∆rT/T2λ=kπ à ∆r=kπ – условие максимума

Геометрическая разность хода равна целому числу.

∆r=2kπ/2 – условие максимума интерференции (k-порядок максимума = 0,1,2,3…)

Геометрическая разность хода ∆r укладывается четное число длин полуволн λ/2. Волны от источника в данную точку приходят в фазе.

A_рез=A₁+A₂=A_max

Если амплитуда равны (A₁=A₂), то А_рез=2A

В этих точках происходит взаимное усиление волн. Эти точки называют максимумами интерференции.

A_рез min если cosФ=0

W∆r/2υ=(2k-1)*π/2

2π∆rT/T2λ=(2k-1)π/2 à ∆r=(2k+1)π/2 – условие минимума (k-порядок минимума = 0,1,2,3…)

Геометрическая разность хода ∆r укладывается нечетное число длин полуволн λ/2. Волны от источника в данную точку приходят в противофазе (∆φ=π; 3π; 5π)

A_рез=⃒A₁-A₂⃒=A_min

Если амплитуда равны (A₁=A₂), то А_рез=0

В этих точках происходит взаимное ослабление волн. Эти точки называют минимумами интерференции.

В остальных точках пространства: Amin < A_рез < A_max

Интерференционная картина – устойчивая во времени и пространстве картина чередования максимумов и минимумов.

Пусть на преграду падает волна, от преграды отразится волна 2.

X

Если 1 плоская волна, то волна 2 тоже плоская.

Волна 1 и 2 когерентны.

При сложении, волны будут интерферировать.

Волны 1 и 2 – бегущие

1-падающая

2-отраженная

S₁=AsinW(t+X/υ)

S₂=AsinW(t-X/υ)-φ₀

φ₀ – фаза появления в результате отражения волны от препятствия.

φ₀ – зависит от соотношения волновых сопротивлений среды.

Волновое сопротивление:

Z=ρ_ср*υ_в

Если 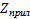» 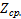, то ₀ = 0

S_рез = S₁ +S₂ = A (sin 𝛼 + sin β) + 2A cos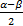* sin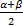= 2A cos() * sin(ωt + =A_рез. * sin(ωt +

В результате сложения двух бегущих волн, мы получили гармоническое колебание с изменяющейся амплитудой и частотой равной частоте падающей волны.

A_{рез .} = max = 2A

Пусть 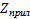» 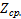, то ₀ =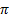

сosФ =1; Ф = =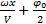

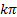
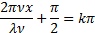
– координаты точек max

A_рез. = 0; cosФ = 0

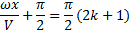
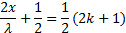
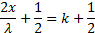
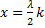– координаты точек min

Таким образом, в результате сложения двух бегучих волн: прямой и обратной – мы получали участки, где амплитуда min – узлы; и участки, где амплитуда max – пучности.

Не меняют положения и постоянны во времени.

Результат сложения прямой и обратной волн – стоячая волна.

Дата добавления: 2014-01-04