Критерии самопроизвольного протекания химического процесса. Энергия Гиббса

Итак, имеем два критерия возможности самопроизвольного протекания химического процесса – изменение энтальпии DН, которое отражает взаимодействие атомов, образование химических связей, то есть определенное упорядочение системы и изменение энтропии DS, которое отражает противоположную тенденцию к беспорядочному расположению частиц. Если DS=0, то движущей силой процесса будет стремление системы к минимуму внутренней энергии, то есть критерий процесса – уменьшение энтальпии или DН<0.

Если DН=0, то критерий самопроизвольного протекания процесса DS>0.

Чтобы иметь возможность количественно сопоставить эти два критерия, нужно, чтобы они выражались в одинаковых единицах (DН – кДж, DS – Дж/К). Очевидно, чтобы выразить энтропийный фактор в единицах энергии, его нужно домножить на температуру. Это тем более логично, что повышение Т способствует увеличению беспорядка в системе. Тогда ТDS – энтропийный фактор процесса, DН – энтальпийный. В состоянии равновесия оба этих фактора должны быть равны:

DН= ТDS. (8.12)

Это уравнение универсально, оно относится и к равновесию жидкость – пар и к другим фазовым превращениям, а также к химическим реакциям. Благодаря этому равенству можно рассчитать изменение энтропии в равновесном процессе, так как при равновесии:

DН/Т = DS.

Однако нас интересует количественный критерий принципиальной возможности протекания процесса. В механике критерий падения тела это уменьшение его гравитационного потенциала, который не зависит от пути перемещения тела. По аналогии химический процесс можно охарактеризовать своим потенциалом, который должен уменьшаться в ходе самопроизвольного процесса. Этот потенциал при постоянной температуре и давлении принято называть изобарно – изотермическим потенциалом Гиббса G. Убыль этого потенциала не зависит от пути процесса и равна максимальной работе, которую можно получить, переходя от данного состояния к равновесному (за вычетом работы против внешнего давления).

-DG=W_рmax. (8.13)

То есть энергия Гиббса – это часть энергетического эффекта химической реакции, которую можно превратить в работу, ее называют свободной энергией.

В таком случае условием возможности протекания процесса будет DG<0, но поскольку в состоянии равновесия DG=0, то из уравнения (1) получаем:

DG=DН - ТDS, (8.14)

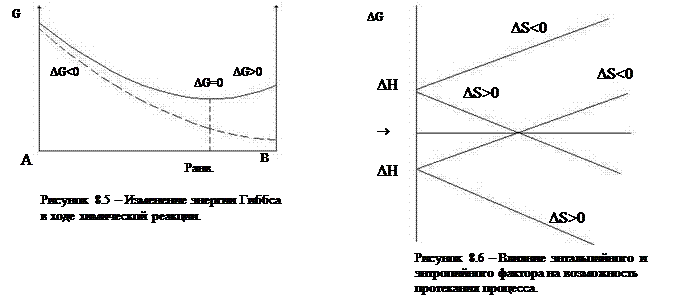
Таким образом, мы определяем G=Н – ТS и можем нарисовать его изменение в ходе процесса (рисунок 8.5):

А«В,

где А – исходные вещества;

В – продукты реакции.

В левой части графика (8.5) – уменьшение значения G, идет прямая реакция. Для нее DG<0. Справа от положения равновесия идет обратная реакция, для нее DG<0. В состоянии равновесия DG=0.

Как влияют величины энтальпийного и энтропийного фактора на протекание процесса?

DG=DН - ТDS

Возможны следующие случаи (рисунок 8.6):

1) экзотермическая реакция, DН<0:

а) DS>0, тогда для любого Т DG будет меньше нуля и процесс идет всегда, причем до конца;

б) DS<0, в этом случае все будет зависеть от соотношения абсолютных значений энтальпийного и энтропийного фактора, DG<0 – реакция идет, DG>0 – реакция не идет.

Экзотермические реакции, сопровождаются уменьшением энтропии, идут при низких температурах, увеличение Т способствует протеканию обратной реакции (Принцип Ле Шателье).

2) Эндотермическая реакция, DН>0:

а) DS>0, реакция возможна только если | ТDS|>|DН|, тогда DG>0, то есть при высоких температурах;

б) если же, DS<0, то DG>0 при любых температурах и процесс самопроизвольно идти не может.

Пример – реакция окисления глюкозы до CO₂ и H₂O:

С₆Н₁₂О₆ + 6О₂ ®6СО₂ + 6Н₂О DН= - 2810 кДж.

Энтропия при этом, очевидно, возрастает. Следовательно, обратный процесс принципиально не может идти самопроизвольно. Для его протекания требуется энергия извне (фотосинтез).

Следует отметить, что в вопросе о возможности протекания процесса термодинамический критерий – истина в последней инстанции. Если изменение значения энергии Гиббса положительные DG>0, никакие катализаторы не помогут провести процесс. При изменении значения энергии Гиббса отрицательные DG<0 процесс может быть заморожен.

До сих пор рассматривали процессы, протекающие при постоянном давлении. Если обратиться к процессам, протекающим при постоянном объеме, получим другое значение термодинамического потенциала – потенциал Гельмгольца:

DF = DU - ТDS, (8.15)

Для решения вопроса о возможности протекания процесса, для расчетов энергии Гиббса DG необходимо установить, от чего она зависит и стандартизировать ее.

Значении DН зависит от температуры и давления и в первом приближении мы считаем, что эта зависимость незначительна и пользуемся стандартными значениями DН°. значение DS кроме давления и температуры зависит еще от концентрации (S=S° - RlnC), следовательно, значение DG также будет зависеть от концентрации реагирующих веществ, а они в ходе процесса меняются. Рассмотрим эту зависимость.

аА®bВ (для простоты)

DG=DН - ТDS, как для всякой реакции.

Считая, что DН слабо зависит от Т, DН = DН° = bDН°_f(B) - aDН°_f(A),

DS = bS(B) – aS(A) = b(S°_B – Rln(B)) – a(S°_A – Rln(A)),

Перегруппировав и вспомнив свойства логарифмов получим:

DS= S° - Rln(B^b/A^a),

Подставив в уравнение для DG, получим

DG=DН° - ТDS° + Rln(B^b/A^a) = DG + RTln(B^b/A^a), (8.16)

Это уравнение изотермы Вант-Гоффа.

где DG°=DН° - ТDS° - термодинамический потенциал, определенный для единичных концентраций или для чистых веществ, то есть стандартный термодинамический потенциал - он определен для единичных концентраций начальных и конечных веществ и для общего давления 1 атм, но может быть разным для разных температур.

Дата добавления: 2014-01-04