Рангова кореляція

Вимірювання тісноти зв'язку за допомогою ко­реляційного і дисперсійного аналізу супроводжується певними складностями і вимагає громіздких обчис­лень. Для орієнтовної оцінки тісноти зв'язку користу­ються наближеними показниками, які не вимагають трудомістких обчислень. До них потрібно віднести: коефіцієнт кореляції знаків Фехнера, коефіцієнт коре­ляції рангів Спірмена і Кендала.

Коефіцієнт кореляції знаків Фехнера визначають на співставленні знаків відхилень від середньої і на підрахунку числа співпадань і неспівпадань знаків.

Коефіцієнт кореляції знаків визначають за форму­лою

де и — число пар с однаковими знаками відхилень х і у від 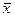і у; v — число пар с різними знаками відхилень х і у від х і у. Коефіцієнт кореляції знаків коли- вається в межах від -1 до +1. Чим ближче до 1, тим" сильніший зв'язок. Знак + або - вказує напрям зв'язку. Якщо и = v, то / = 0 і зв'язку немає.

Приклад 5.4 [18]

Таблиця 5.5

Вартість основних фондів (ОФ) та випуск продукції (млн грош, од.)

№ Підпри­ємства	Вартість ОФ М	Випуск про­дукції (у)	Знак відхилення
х-х	у-у
		2,4	_	_
		4,0	_	_
		3,6	_	_
		4,0	_	__
		4,5	_	_
		4,6	+	_
		5,6	+	+
		6,5	+	+
		7,0	+	+
		5,0	+	+
Разом		47,2	х	х

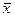= 108/10 = 10,8 млн. грош, од.,

= 47,2/10 = 4,72 млн. грош. од.

Таким чином, u = 9, v = 1. Тоді

Це означає, що зв'язок між вартістю основних фондів та випуском продукції прямий та досить тіс­ний.

Розглянемо ще один метод оцінки тісноти зв'язку ца основі розрахунку коефіцієнта кореляції рангів. Його основна відмінність полягає в тому, що він об-цислюється не на основі первинних даних, а на основі рангів, які присвоюються всім значенням дослід­жуваних ознак, що розміщені у порядку зростання. Якщо значення співпадають, то ранг визначається шляхом ділення суми рангів на число значень.

Коефіцієнт кореляції рангів Спірмена визначається за формулою

де d² - квадрат різниці рангів для кожної одиниці d = х — у; п — обсяг сукупності.

Коефіцієнт кореляції рангів Спірмена також коли­вається від -1 до +1. Чим ближче до 1, тим тісніший зв'язок. Знак + або — вказує напрям зв'язку. Якщо ранги за обома ознаками співпадають, то зв'язок пря­мий. Якщо ρ =0, то зв'язок між ознаками відсутній. Обчислимо коефіцієнт кореляції рангів за даними по­переднього прикладу (табл. 5.6).

Таблиця 5.6

Розрахунок коефіцієнта кореляції рангів Спірмена

ранги	Ранги по х	Ранги по у	Різниця рангів	d^2
		3.5	-1.5	2.25
			+1
	4.5	3.5	+1
	4.5		-0.5	0.25
			-1
			-1
			-1
			+3
Разом	X	х	X	16.5

Ранги вартості основних фондів для четвертого та п'ятого підприємств визначалися як середня арифме-тична з х = (4+5)/2 = 4,5. Аналогічно для другого i четвертого за випуском продукції. Підставивши у формулу, отримаємо:

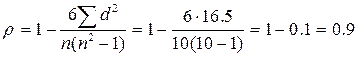
Коефіцієнт кореляції свідчить, що зв'язок між вар­тістю основних фондів та випуском продукції прямий та тісний.

Ранговий коефіцієнт кореляції більш точний порівняно з коефіцієнтом кореляції знаків, тому що він враховує не тільки знаки відхилень, а й місце ве­личини ознаки в даному ряду.

Окрім вище згаданих коефіцієнтів, на практиці для визначення рейтингу і оцінки тісноти зв'язку викори­стовують коефіцієнт кореляції рангів Кендала:

Де s_i - сума балів

Суть даного методу полягає в підрахунку числа балів для кожної одиниці сукупності. Для цього ранг першої одиниці сукупності за ознакою у в упоряд­кованому по де ряду порівнюємо з усіма іншими оди­ницями сукупності, які розміщені нижче в списку. Якщо він менше першої бдиниці сукупності, при­своюємо йому +1 бал, якщо більше — присвоюємо — 1.

Розглянемо на прикладі 5.4 обчислення коефі­цієнта Кендала (табл. 5.7):

Отриманий коефіцієнт свідчить про наявність до­сить тісного прямого зв'язку між вартістю основних фондів і обсягом випуску продукції. Критичне зна­чення коефіцієнта Кендала для рівня значимості 0= 0,05 при п = 10 дорівнює 0,467. Фактичне значен­ня більше за критичне, що підтверджує зроблений раніше висновок про існування зв'язку між згаданими явищами.

Таблиця 5.7

Підрахунок числа балів

	• V
№.	Ранги	• Бали (З;,)
пох	по у	S1i	S2i	S3i	S4i	S5i	S6l	S7i	S8i	S9i
			+1
			+1	-1]
			+1	+1	+1
			+1	+1	+1	+1
	б		+1	+1	+1	+1	+1
			+1	+1	+1	+ 1	+1	+1
			+1	+1	+1	+ 1	+1	+1	+1
			+1	+1	+1	+ 1	+1	+1	+1	+1
			+1	+1	+1	+ 1	+1	+1	-1	-1	-1
	X	X	+9	+6	+7	+6	+5	+3	+1		-1

Питання для самоконтролю.

1. Чому суми граф 4 і 5 табл. 5.1 мають однакові абсолютні зна­чення?

2. Наведіть три приклади статистичного зв'язку.

3. Про що свідчить факт, коли групові середні, обчислені при дисперсійному аналізі, мають однакові значення?

4. Який зв'язок зветься кореляційним, який стохастичним? На­ведіть приклади.

5. Що таке кореляція; регресія?

6. Наведіть приклад кореляційного зв'язку, форму якого можна відобразити параболою другого порядку.

7. Наведіть приклад кореляційного зв'язку у формі гіперболи, степеневої функції.

8. За даними соціологічного опитування 10 студентів проранго-вані по двом ознакам — «активність під час занять» та «оцінка»:

Ознака	№ студента
Активність			4,
Оцінка

Оцініть тісноту зв'язку між ознаками.

9. На підставі таких даних визначіть наявність зв'язку між озна­ками «місячний заробіток — вік робітника»:

Місячний заробіток, грн.	Число робітників у віці, років	Разом
20-35	35-50	більше 50
200-400
400-600
600-800
800-1000

10 Визначити наявність зв'язку між ознаками А і В:

A	В
В1	В2	ВЗ
А1
А2

11. На підставі таких даних визначити наявність зв'язку між оз­наками:

Сімейне становище	Наявність окремої квартири
Мають	Не мають
Сімейні
Одинокі		ЗО

12. На підставі таких даних вивчити взаємозв'язок між спе­ціальністю та денним заробітком, грн. [4]:

№ п/п	Спеціальність	Денний заробіток	№ п/п	Спеціальність	Денний заробіток
	Токар	10,42		Токар	9,66
	Слюсар	9,54		Фрезерувальник	6,84
	Фрезерувальник	10,05		Фрезерувальник	10,24
	Фрезерувальник	8,12		Слюсар	13,53
	Слюсар	8,45		Фрезерувальник	9,83
	Фрезерувальник	7,54		Токар	11,33
	Токар	12,25		Фрезерувальник	8,74
	Слюсар	11,22		Слюсар	10,34
	Фрезерувальник	9,32		Фрезерувальник	7,96
	Токар	14,15		Слюсар	9,77

13. Назвіть два приклади, коли гіпотезу про однорідність до­цільніше замінити гіпотезою про незалежність.

14. З яких міркувань вибирається значення рівня істотності при перевірці гіпотез?

15. Які існують прості методи оцінки тісноти взаємозв'язку між ознаками?

16. Чим відрізняються один від другого коефіцієнти кореляції Спірмена та Кендала?

17. В яких випадках застосовують коефіцієнт асоціації?

18. У чому недосконалість методу кореляції знаків?

19. Маємо дані про середній бал 10 студентів на вступних іспиті^ та на першій екзаменаційній сесії [4]:

№п/п	Середній бал	№ п/п	Середній бал
на Іспитах	на сесії	на Іспитах	на сесії
	4,8	4,7		3,3	4,1
	4,4	4,2		4,0	3,7
	4,2	4,4		3,9	3,0
	5,0	5,0		4,7	4,3
	4,5	4,9		3,7	3,2 ~~

Визначіть тісноту зв'язку між середніми балами, використо­вуючи коефіцієнти рангової кореляції Спірмена та Кендала (а = 0,05) [4].

20. На основі таких даних визначити, чи є зв'язок між курінням та станом легень:

Значення проби легеневої	Відношення до куріння
не курять	курять	ті, що кинули
Нормальне
Не нормальне

21. Із групи 112 критично хворих людей, які знаходились у реа­німаційному відділенні, в стані шоку перебувало 77 чол., з яких 37 померли. Відомо 5 типів шоку. На підставі таких да­них визначити; чи залежить шанс вижити від наявності шоку та його типу.

Тип шоку	Шанс вижити
вижили	не вижили
Гіпо
Карді
Невро
Септи
Ендо
Відсутній
Разом

ТЕМА 6 Ряди динаміки

Дата добавления: 2014-01-04