
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теоремы о дифференцируемых функциях
|
|
|
|
Лекция 13.
ПЛАН
1. Введение.
2. Теорема Ферма. Наибольшее и наименьшее
значения функции на отрезке.
3. Теорема Ролля.
4. Теорема Лагранжа – теорема о среднем значении.
5. Теорема Коши об отношении приращений.
6. Правило Лопиталя для раскрытия неопределенностей вида.
13.1. Введение
Как только стало возможным определить скорость изменения функции с помощью производной – пытливое человечество (в лице аристократов математиков) тут же стало возводить храм «Дифференциального исчисления», фундаментом которого являются теоремы Ферма, Ролля, Лагранжа, Коши, Лопиталя, Тейлора. Бегло осмотрим их наследие, взяв на заметку (и на вооружение) то, что может пригодиться нам в дальнейшем.
13.2. Теорема Ферма. Наибольшее и наименьшее
значение функции на отрезке
Теорема 13.1 (теорема Ферма). Пусть функция 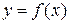 определена и дифференцируема на интервале
определена и дифференцируема на интервале  и в некоторой точке
и в некоторой точке  принимает наибольшее (наименьшее) значение. Тогда производная в этой точке
принимает наибольшее (наименьшее) значение. Тогда производная в этой точке  будет равна нулю.
будет равна нулю.
 Доказательство.
Доказательство.
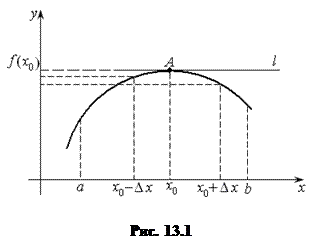
Рассмотрим функцию  , отвечающую теореме Ферма, и принимающую в точке
, отвечающую теореме Ферма, и принимающую в точке  наибольшее значение (рис. 13.1). Тогда для этой точки справедливо неравенство
наибольшее значение (рис. 13.1). Тогда для этой точки справедливо неравенство 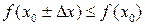 для всех x из некоторой окрестности точки x 0.
для всех x из некоторой окрестности точки x 0.
Найдем производную 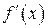 в точке
в точке  , воспользовавшись определением:
, воспользовавшись определением:
 .
.
Если  слева, то D x будет меньше нуля, приращение
слева, то D x будет меньше нуля, приращение  , а их отношение
, а их отношение 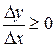 .
.
Если  справа, то
справа, то 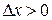 ,
,  и
и 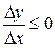 .
.
Запишем это в общем виде:

Но 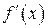 не должна зависеть от способа стремления
не должна зависеть от способа стремления 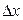 к нулю. Поэтому, если
к нулю. Поэтому, если 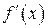 дифференцируема, то ее производная в точке
дифференцируема, то ее производная в точке  может быть равна только нулю, что и требовалось доказать.
может быть равна только нулю, что и требовалось доказать.
Геометрически теорему Ферма можно пояснить так. Если  – точка, в которой функция принимает наибольшее для интервала
– точка, в которой функция принимает наибольшее для интервала  значение, то касательная в точке
значение, то касательная в точке 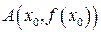 будет параллельна оси
будет параллельна оси  (рис. 13.1). Но
(рис. 13.1). Но 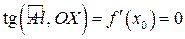 , что и следовало из теоремы.
, что и следовало из теоремы.
Кинетически теорема Ферма означает, что в точках наибольшего и наименьшего значений скорость изменения функции равна нулю. Она как бы застывает в этой точке перед последующим падением или взлетом.
Позднее эти точки назовут экстремальными и теорему Ферма (без указания авторства) будут применять для их нахождения. Такова жизнь.
Вопросы к размышлению (для отличников).
 1. Будет ли верна теорема Ферма, если интервал
1. Будет ли верна теорема Ферма, если интервал  заменить отрезком
заменить отрезком 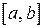 ?
?
2. Будет ли верна теорема Ферма для функции на рис. 13.2? Какие условия нужно добавит в теорему?
3. Будет ли верна обратная теорема, которая формулируется так: пусть функция 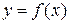 непрерывна и дифференцируема на интервале
непрерывна и дифференцируема на интервале  и в некоторой точке
и в некоторой точке  ее производная обращается в нуль. Тогда точка
ее производная обращается в нуль. Тогда точка  – точка экстремума.
– точка экстремума.
Для иллюстрации (или опровержения) этой теоремы приведите соответствующие примеры и тогда вам все станет ясно.
А теперь дадим правило для нахождения наибольшего и наименьшего значений функции 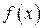 на отрезке
на отрезке 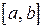 .
.
Для того, чтобы найти  и
и  , нужно найти точки, где
, нужно найти точки, где 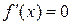 , либо не существует, а также
, либо не существует, а также  и
и  . Из найденных значений выбрать наименьшее и наибольшее.
. Из найденных значений выбрать наименьшее и наибольшее.
Пример 13.1. Найти наибольшее и наименьшее значение функции  на отрезке
на отрезке  .
.
Решение.
1. Найдем 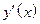 , и точки, где
, и точки, где 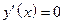 .
.
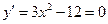 , если
, если  .
.
Обе точки принадлежат рассматриваемому интервалу.
2. Найдем  и
и 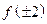 и сравним полученные результаты.
и сравним полученные результаты.


Теорему Ферма иногда называют теоремой о корнях производной. Напомним, что корнем функции  называется точка, где
называется точка, где  и график пересекает ось
и график пересекает ось  . Вернитесь в прошлую лекцию, п. «Графическое дифференцирование». График функции
. Вернитесь в прошлую лекцию, п. «Графическое дифференцирование». График функции 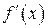 пересекает ось
пересекает ось  в точке максимального значения.
в точке максимального значения.
Следующая теорема ничего нового для нахождения экстремальных точек не даст, но она необходима для доказательства последующих теорем Лагранжа и Коши, которые, как мы увидим, имеют уже практическое значение.
13.3. Теорема Ролля
Теорема 13.2 (теорема Ролля). Если функция 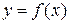 непрерывна и дифференцируема на отрезке
непрерывна и дифференцируема на отрезке 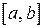 и на концах отрезка обращается в нуль, т.е.
и на концах отрезка обращается в нуль, т.е.  , то внутри этого отрезка найдется хотя бы одна точка
, то внутри этого отрезка найдется хотя бы одна точка  , в которой производная равна нулю
, в которой производная равна нулю 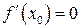 .
.
 Геометрическая иллюстрация этой теоремы приведена на рис. 13.3.
Геометрическая иллюстрация этой теоремы приведена на рис. 13.3.
Доказательство. Так как функция  непрерывна на отрезке
непрерывна на отрезке 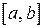 , то она на этом отрезке достигает наибольшего и наименьшего значений
, то она на этом отрезке достигает наибольшего и наименьшего значений 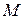 и
и  (см. теоремы о непрерывных функциях в лекции 10).
(см. теоремы о непрерывных функциях в лекции 10).
Если эти значения достигаются на концах отрезка, то это означает,  , т.е. функция является постоянной, производная от которой равна нулю.
, т.е. функция является постоянной, производная от которой равна нулю.
Пусть одно из чисел, например M, достигается внутри отрезка 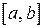 . Значение аргумента
. Значение аргумента 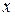 в этой точке
в этой точке 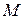 обозначим через
обозначим через  . Поскольку функция в этой точке дифференцируема, то по теореме Ферма
. Поскольку функция в этой точке дифференцируема, то по теореме Ферма 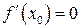 , что и требовалось доказать.
, что и требовалось доказать.
Но существуют еще две точки, в которых производная обращается в нуль – это точки 
 , поэтому в условии теоремы написано «хотя бы одна точка…»
, поэтому в условии теоремы написано «хотя бы одна точка…»
Вообще в теоремах нет лишних слов. Каждое слово означает требование, которое следует выполнить.
Для иллюстрации этого положения рассмотрим функцию  на отрезке
на отрезке 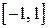 . Она непрерывна на этом отрезке и
. Она непрерывна на этом отрезке и 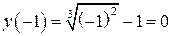 и
и  , т.е. два условия теоремы выполнены. Найдем
, т.е. два условия теоремы выполнены. Найдем  .
.
Эта производная нигде не обращается в нуль. Что же, теорема Ролля не верна? Верна.
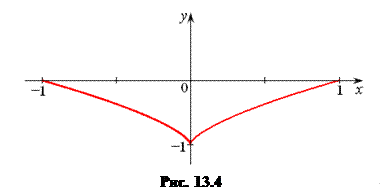 Мы забыли еще одно требование – требование дифференцируемости. В точке
Мы забыли еще одно требование – требование дифференцируемости. В точке 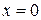 ,
, 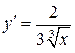 не существует, т.е.
не существует, т.е.  не дифференцируема и, следовательно, применить к ней теорему Ролля нельзя. График функции
не дифференцируема и, следовательно, применить к ней теорему Ролля нельзя. График функции  изображен на рис. 13.4.
изображен на рис. 13.4.
Так математика учит нас зоркому отношению к «мелочам».
А теперь вопросы.
1. Как измениться формулировка теоремы Ролля для функции, изображенной на рис. 13.4.?
2. Будет ли верна теорема Ролля, если условие 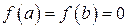 заменить на
заменить на  ?
?
Следующую теорему используют для доказательства многих важных теорем, поэтому отнеситесь к ней внимательно.
13.4. Теорема Лагранжа о среднем значении
Теорема 13.3 (теорема Лагранжа). Если функция 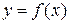 непрерывна и дифференцируема на отрезке
непрерывна и дифференцируема на отрезке 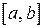 , то внутри этого отрезка найдется хотя бы одна точка
, то внутри этого отрезка найдется хотя бы одна точка  , в которой производная равна отношению приращения функции
, в которой производная равна отношению приращения функции 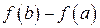 к приращению аргумента
к приращению аргумента  :
:
 . (13.1)
. (13.1)
Геометрическая интерпретация этой теоремы дана на рис. 13.5.
 Пусть
Пусть 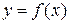 непрерывна и дифференцируема на отрезке
непрерывна и дифференцируема на отрезке 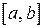 . Проведем хорду
. Проведем хорду 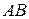 , получим
, получим  , в котором
, в котором  ,
, 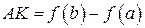 и тангенс угла наклона хорды
и тангенс угла наклона хорды 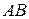 равен
равен 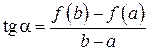 . Теорема утверждает, что найдется хотя бы одна точка
. Теорема утверждает, что найдется хотя бы одна точка  на графике функции
на графике функции  , в которой касательная параллельна хорде или
, в которой касательная параллельна хорде или  .
.
Доказательство.
Для доказательства теоремы Лагранжа используем прием, которым часто пользуются в математике – введение дополнительной функции, обладающей заданными свойствами. В ней обязательно должно присутствовать выражение, входящее в доказательство  . Эта дополнительная функция похожа на обертку – сохраняет и доставляет товар покупателю и сразу исчезает, как только товар начинают применять по назначению.
. Эта дополнительная функция похожа на обертку – сохраняет и доставляет товар покупателю и сразу исчезает, как только товар начинают применять по назначению.
Итак, введем дополнительную функцию
 . (13.2)
. (13.2)
Запишем уравнение хорды 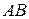 , как уравнение прямой, проходящей через данную точку
, как уравнение прямой, проходящей через данную точку 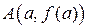 и заданным угловым коэффициентом
и заданным угловым коэффициентом
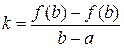 ,
,
 . (13.3)
. (13.3)
Подставим (13.3) в (13.2), получим:
 . (13.4)
. (13.4)
Функция  отвечает всем условиям теоремы Ролля:
отвечает всем условиям теоремы Ролля:  – непрерывна, дифференцируема и
– непрерывна, дифференцируема и  (подставьте и убедитесь). Следовательно, существует такая точка
(подставьте и убедитесь). Следовательно, существует такая точка  , в которой
, в которой  . Находим
. Находим 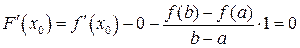 . Отсюда
. Отсюда  , что и требовалось доказать.
, что и требовалось доказать.
Формула (13.1) иногда записывается в следующем виде:
 (13.5)
(13.5)
и читают так: приращение 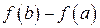 функции на отрезке
функции на отрезке 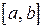 равно произведению длины этого отрезка
равно произведению длины этого отрезка  на значение производной от этой функции в некоторой внутренней точке
на значение производной от этой функции в некоторой внутренней точке  –
–  .
.
Аналог этой формулы мы встретим и в интегральном исчислении, когда будем знакомиться со свойствами определенного интеграла
 .
.
Подобные формулы существуют и в двойных и в тройных интегралах. Их называют теоремами о среднем значении. О каком же «среднем» значении идет речь в теореме Лагранжа?
Вспомним механический смысл производной. Если 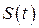 – путь, пройденный точкой от начального положения, то
– путь, пройденный точкой от начального положения, то 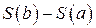 есть путь, пройденный с момента
есть путь, пройденный с момента  по момент
по момент  , а отношение
, а отношение  – средняя скорость за этот промежуток времени. Причем неважно, какие зигзаги делал этот путь – важны начальная
– средняя скорость за этот промежуток времени. Причем неважно, какие зигзаги делал этот путь – важны начальная 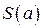 и конечная
и конечная  точки. Поэтому и
точки. Поэтому и  – это скорость в серединной (или очень близкой к ней) точке отрезка
– это скорость в серединной (или очень близкой к ней) точке отрезка 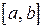 . Интересный результат, правда? Мы его потом используем в экономике.
. Интересный результат, правда? Мы его потом используем в экономике.
Пример 13.2. На кривой 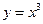 найти точку, в которой скорость изменения имеет среднее значение на отрезке
найти точку, в которой скорость изменения имеет среднее значение на отрезке 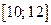 .
.
Решение. Запишем формулу Лагранжа с учетом, что 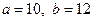 и
и  .
.
 ,
,
т.е. близко к середине отрезка 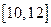 . Число 364 – это скорость. Она может измеряться в км/ч, если x измеряется в часах, y в километрах; руб./мес., если y – это деньги, x – время в месяцах и т.д.
. Число 364 – это скорость. Она может измеряться в км/ч, если x измеряется в часах, y в километрах; руб./мес., если y – это деньги, x – время в месяцах и т.д.
Следующая теорема является обобщением теоремы Лагранжа на случай двух функций 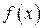 и
и  . Она позволяет сравнивать скорости изменения этих функций на отрезке
. Она позволяет сравнивать скорости изменения этих функций на отрезке 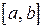 с результатами приращений. Интуитивно ясно, чем больше приращение, тем больше скорость. Именно об этом говорит теорема Коши.
с результатами приращений. Интуитивно ясно, чем больше приращение, тем больше скорость. Именно об этом говорит теорема Коши.
13.5. Теорема Коши об отношении приращений
Теорема 13.4 (теорема Коши). Если функции  и
и 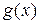 непрерывны и дифференцируемы на отрезке
непрерывны и дифференцируемы на отрезке 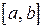 , причем
, причем  и
и 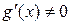 , то внутри этого отрезка найдется хотя бы одна точка
, то внутри этого отрезка найдется хотя бы одна точка  , для которой выполняется равенство:
, для которой выполняется равенство:
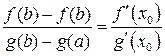 . (13.6)
. (13.6)
То есть пути, пройденные функциями  и
и 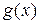 в промежуток
в промежуток 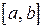 относятся как скорости в какой-то промежуточной точке
относятся как скорости в какой-то промежуточной точке  , одинаковой для обеих функций.
, одинаковой для обеих функций.
Доказательство. Доказывают эту теорему с помощью введения вспомогательной функции
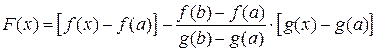 , (13.7)
, (13.7)
которая отвечает теореме Ролля:  (проверьте, вместо
(проверьте, вместо 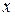 подставив
подставив  и
и 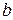 ), непрерывна и дифференцируема, как и
), непрерывна и дифференцируема, как и  и
и 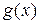 , поэтому найдется хотя бы одна точка
, поэтому найдется хотя бы одна точка  , в которой
, в которой  .
.
Находим 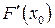 для равенства (13.7):
для равенства (13.7):
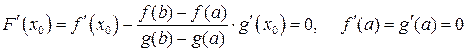
как производные от постоянных. Откуда и получаем формулу (13.6).
Должны сказать, что доказательств всех четырех вышеизложенных теорем существует множество, поэтому мы не стали приводить их здесь, в этом пособии. Найдите их в учебнике, придумайте свое – выбор за вами, но результат должен быть.
А теперь вопрос: можно ли было доказать теорему Коши с помощью простого деления левой части (и числителя и знаменателя) на  , вот так:
, вот так:
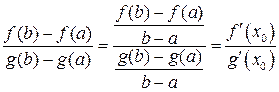 ?
?
Та ли это точка  , о которой шла речь в теореме Лагранжа (приблизительно середина отрезка
, о которой шла речь в теореме Лагранжа (приблизительно середина отрезка 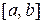 )? Подумайте. А пока пример.
)? Подумайте. А пока пример.
Пример 13.3. Две фирмы в течении двух лет  , получали прибыль по законам: первая
, получали прибыль по законам: первая  , вторая
, вторая 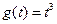 . Во сколько k раз вторая фирма получит больше прибыли на конец 2 года и в какой промежуток времени скорости их обогащения будут также равны k?
. Во сколько k раз вторая фирма получит больше прибыли на конец 2 года и в какой промежуток времени скорости их обогащения будут также равны k?
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1492; Нарушение авторских прав?; Мы поможем в написании вашей работы!