Решение. а) Найдем приращение прибылей для каждой фирмы:

а) Найдем приращение прибылей для каждой фирмы:

I. ,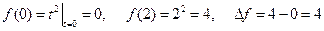

II. .

б) Найдем число k:

.

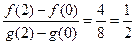Следовательно вторая фирма получит в 2 раза больше прибыли, чем первая.

в) Найдем отношение скоростей обогащения и точку, в которой .

, , .

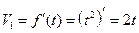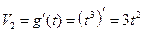По условию 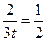, откуда . То есть в момент времени 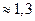года скорости их обогащения будут равны .

Ну и, наконец, еще одна теорема, которая имеет практическое приложения для вычисления различных пределов.

13.6. Правило Лопиталя. Раскрытие неопределенностей

Теорема 13.5 (правило Лопиталя). Пусть функции и – бесконечно малые величины при () и их отношение дает неопределенность . Если существует предел отношения производных этих функций 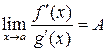, то к такому же пределу будет стремиться и отношение 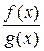, т.е.

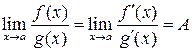. (13.8)

Если 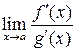– так же даст неопределенность 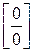, то к нему можно применить правило Лопиталя еще раз.

Обращаем ваше внимание, что в формуле (13.8) присутствует именно частное производных, а не производная частного.

Доказывается эта теорема с помощью теоремы Коши для отрезка .

Правило Лопиталя можно использовать и в случае неопределенностей типа 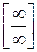. Главное, на каждом этапе проверять имеем ли мы еще неопределенности указанных видов или нет, т.к. 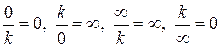, если – число и к этим выражениям применять правило Лопиталя нельзя.

Примеры 13.4. Вычислить пределы, используя правило Лопиталя.

1. .

2. .

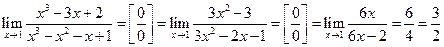В данном примере мы дважды использовали правило Лопиталя.

3. .

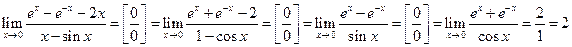Применение правила Лопиталя можно комбинировать с преобразованиями и прямой подстановкой предельных значений к части подпредельного выражения.

4. .

Преобразуем выражение 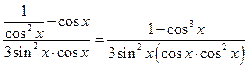. Учтем, что и тогда под знаком предела останется выражение . Применим к нему правило Лопиталя:

.

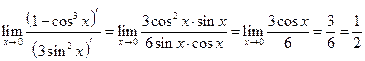5. .

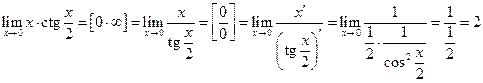Можно ли применить правило Лопиталя к неопределенностям вида . Да, можно, но предварительно выражение нужно прологарифмировать.

6. .

Предположим, что предел этого выражения существует и равен А, то есть 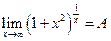. Прологарифмируем обе части равенства.

Сведем начало и конец воедино.

, то есть .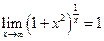

Дата добавления: 2014-01-04