
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Исследование поведения функции
|
|
|
|
Лекция 14.
Следует помнить, что в каком-то смысле высшая математика проще элементарной. Исследовать, например, лесную чащу пешком очень трудно, а с самолета это делается проще.
У. Сойер
(английский математик и педагог)
ПЛАН
1. Введение.
2. Область определения функции.
3. Симметрия, точки пересечения с осями координат.
4. Интервалы возрастания и убывания функции.
5. Точки экстремума. Необходимые и достаточные условия.
6. Введение. Общий план исследования функции.
7. Выпуклость и вогнутость формы графика. Точки перегиба.
8. Асимптоты функции.
9. Пример исследования функции.
10. Заключение.
14.1. Введение
Было бы наивно полгать, что все «измышления» (теоремы, правила и т.д.) дифференциального исчисления практичное человечество не смогло поставить себе на службу. Сокровища науки только до поры остаются известными узким специалистам. Приходит время, и ими начинают пользоваться многие, приспосабливая к своим задачам.
Любое явление – конъюнктура рынка, сезонные колебания спроса на товар, прибыль и т.д. – вначале изучаются с количественной стороны, а потом, если это, возможно, описывают функциональной зависимостью, т.е. формулой.
Например, анализ спроса на купальники показал, что он подчиняется формуле 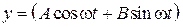 , где
, где 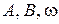 – некоторые постоянные, не меняющиеся в течении лет,
– некоторые постоянные, не меняющиеся в течении лет, 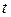 – время (мес.). На основании приведенной формулы можно выяснить, при каких значениях
– время (мес.). На основании приведенной формулы можно выяснить, при каких значениях 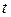 спрос будет максимальным и каких именно величин он достигнет, при каких – минимальным и ряд других вопросов.
спрос будет максимальным и каких именно величин он достигнет, при каких – минимальным и ряд других вопросов.
Именно они входят в понятие «исследование поведение функции». Очевидно, выяснять эти вопросы с помощью самостоятельного сбора информации не всегда разумно, а иногда затруднительно. Поэтому в данной главе покажем общие приемы исследования функций. За основу возьмем аналитический способ задания, а потом, при решении экономических задач, используем табличный и графический способы, как наиболее часто встречающиеся. Все исследования подчиним общему плану, каждый пункт которого будет решать свои задачи, подкрепленные соответствующими теоретическими обоснованиями. Итак, план.
План исследования функции.
1. Область определения функции. Выявление точек разрыва, поведение функции вблизи точек разрыва.
2. Симметрия, точки пересечения с осями координат.
3. Интервалы возрастания – убывания, точки экстремумов (первая производная)
4. Интервалы выпуклости – вогнутости, точки перегиба (вторая производная)
5. Асимптоты: вертикальные, горизонтальные, наклонные.
6. Построение графика.
Некоторые из разделов уже рассматривались в той или иной мере. Вспомним, что знаем и дополним то, чего не знаем.
14.2. Область определения функции
Область определения функции или область допустимых значений (ОДЗ) рассматривалась в лекции 8 «Функции. Способы задания».
Напомним, что если функция задана аналитически, т. е. с помощью формулы, то соблюдают требования:
1) неотрицательности подкоренного выражения: если 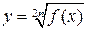 , то
, то 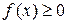 ;
;
2) положительности подлогарифмического выражения: если 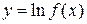 , то
, то 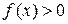 , и
, и
3) неравенства нулю знаменателя дроби: если 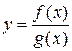 , то
, то 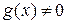 .
.
Например:
1. 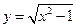 ОДЗ
ОДЗ 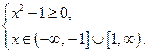
2. 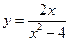 ОДЗ
ОДЗ 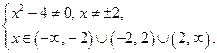
Рассмотрим последний пример подробнее, определив поведение функции вблизи точек разрыва  и
и 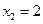 . Для этого найдем односторонние пределы при
. Для этого найдем односторонние пределы при 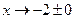 и
и 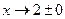 .
.
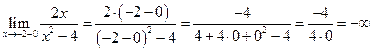 ,
,
 ,
,
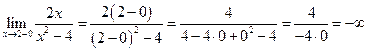 ,
,
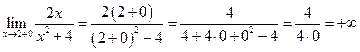 .
.
Нарисуем соответствующий график:
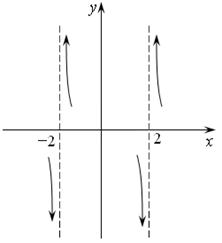
Рис. 14.1.
Как ведет себя функция в остальных точках мы не знаем, поэтому торопиться с общим графиком не будем. Мы исследуем ее по полной программе, в качестве иллюстрирующего примера.
14.3. Симметрия, точки пересечения с осями координат
За симметрию графика относительно осей или начала координат отвечает четность и нечетность функции.
Функция 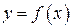 называется четной, если для нее справедливо равенство
называется четной, если для нее справедливо равенство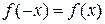 и нечетной, если
и нечетной, если 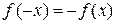 .
.
Четные функции симметричны относительно оси 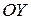 , нечетные – относительно начала координат, т.е. точки
, нечетные – относительно начала координат, т.е. точки 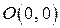 .
.
Четные функции – это 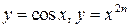 . Нечетные –
. Нечетные – 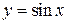 ,
, 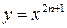 .
.
Полезно помнить, что если в аналитическое выражение функции входит произведение или частное четных и нечетных функций, то можно пользоваться правилом знаков, т.е. произведение (частное) одноименных (либо четных, либо нечетных) функций есть функция четная, разноименных – нечетная.
Поэтому функция 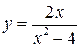 – нечетная, т.к.
– нечетная, т.к. 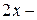 нечетная,
нечетная, 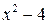 – четная,
– четная, 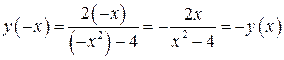 , и ее график симметричен относительно точки
, и ее график симметричен относительно точки 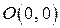 . Аналогично
. Аналогично 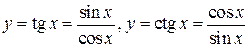 – нечетные функции.
– нечетные функции.
К сумме и разности это свойство неприменимо. Функции, не обладающие свойством симметрии, называют функциями общего вида.
Точки пресечения графика 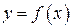 с осями координат находятся из решения уравнений:
с осями координат находятся из решения уравнений: 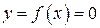 – точки пересечения с осью
– точки пересечения с осью  (их называют корнями),
(их называют корнями), 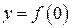 – точки пересечения с осью
– точки пересечения с осью 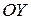 .
.
У нечетных функций точка 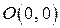 является и корнем и точкой пересечения с осью
является и корнем и точкой пересечения с осью 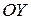 .
.
Для нашей функции 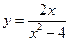 , если
, если 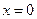 , то
, то 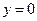 , что и следовало ожидать, и других точек пересечения с осями координат нет:
, что и следовало ожидать, и других точек пересечения с осями координат нет: 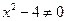 . Поэтому ее график будет выглядеть так (рис. 14.2):
. Поэтому ее график будет выглядеть так (рис. 14.2):
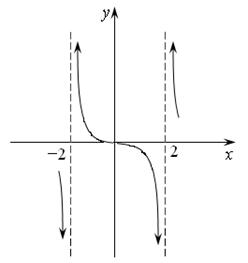
Рис. 14.2.
Отысканием корней вы много занимались в школе и мы рассказывали о методе половинного деления (см. лекцию 10), поэтому подробно на этом моменте останавливаться не будем.
14.4. Интервалы возрастания и убывания функции
Определение 14.1. Функция 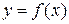 , непрерывная на интервале
, непрерывная на интервале  называется возрастающей, если большему значению аргумента
называется возрастающей, если большему значению аргумента 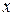 соответствует большее значение
соответствует большее значение 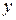 , т. е. из выполнения неравенства
, т. е. из выполнения неравенства 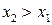 следует выполнение неравенства
следует выполнение неравенства 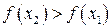 .
.
Определение 14.2. Функция 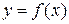 , непрерывная на интервале
, непрерывная на интервале  называется убывающей, если большему значению аргумента
называется убывающей, если большему значению аргумента 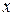 соответствует меньшее значение
соответствует меньшее значение 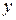 , т. е. из выполнения неравенства
, т. е. из выполнения неравенства 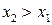 следует выполнение неравенства
следует выполнение неравенства 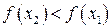 .
.
Теорема 14.1 (необходимое условие возрастания функции). Пусть функция 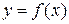 дифференцируема на отрезке
дифференцируема на отрезке 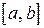 . Для того, чтобы она была всюду возрастающей на этом отрезке необходимо, чтобы ее первая производная
. Для того, чтобы она была всюду возрастающей на этом отрезке необходимо, чтобы ее первая производная 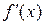 была всюду неотрицательна, т.е.
была всюду неотрицательна, т.е. 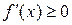 .
.
Доказательство.
Дано: 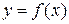 – возрастает на отрезке
– возрастает на отрезке 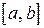 .
.
Доказать: 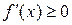 (рис. 14.3).
(рис. 14.3).
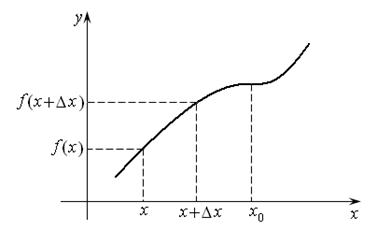
Рис. 14.3
1. Возьмем произвольную точку 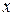 и дадим аргументу положительное приращение
и дадим аргументу положительное приращение 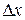 . Тогда
. Тогда 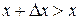 и
и 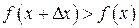 по условию.
по условию.
2. Рассмотрим отношение приращения функции 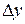 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента 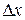 :
:
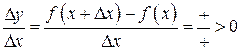 (нас интересует знак).
(нас интересует знак).
3. Найдем предел этого отношения при  :
:
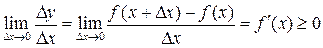 .
.
Откуда взялся знак равенства? Он возник в точках, где приращение 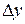 не просто стремиться к нулю, а равно нулю при
не просто стремиться к нулю, а равно нулю при  , как в точке
, как в точке  .
.
Таким образом, необходимое условие возрастания функции доказано. Сформулируем и докажем теперь достаточное условие возрастания функции.
Теорема 14.2 (достаточное условие возрастания функции). Пусть функция 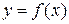 дифференцируема на отрезке
дифференцируема на отрезке 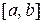 и ее производная
и ее производная 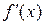 всюду положительна, т.е.
всюду положительна, т.е. 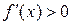 . Тогда функция
. Тогда функция  будет всюду возрастающей.
будет всюду возрастающей.
Доказательство.
Дано: 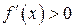 на отрезке
на отрезке 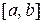 .
.
Доказать: 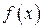 – возрастает на этом интервале.
– возрастает на этом интервале.
1. Возьмем две произвольные точки: 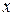 и
и 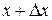 , где
, где 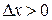 .
.
2. Рассмотрим разность 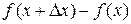 . Напишем для нее формулу Лагранжа (а вы думали, что мы о ней забудем до экзамена?). Итак,
. Напишем для нее формулу Лагранжа (а вы думали, что мы о ней забудем до экзамена?). Итак, 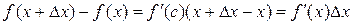 .
.
3. По условию 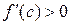 , и
, и 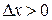 по нашему выбору (см. п. 1), поэтому произведение
по нашему выбору (см. п. 1), поэтому произведение 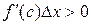 .
.
4. Но тогда и 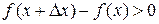 (левая и правая части равенства всегда имеют одинаковые знаки), т. е.
(левая и правая части равенства всегда имеют одинаковые знаки), т. е. 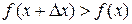 , что и говорит о возрастании
, что и говорит о возрастании  .
.
Таким образом, необходимое и достаточное условия возрастания функции нами полностью доказаны. Запишем формулировки рассмотренных теорем символически следующим образом:
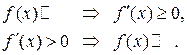
Вопросы для размышления.
1. Являются ли теоремы 14.1 и 14.2 взаимно обратными? В чем между ними различие?
2. Как изменятся формулировки этих теорем, если мы будем рассматривать не строго возрастающие функции? Можно ли их объединить в одну теорему?
Аналогично доказываются необходимое и достаточное условия убывания функции.
Теорема 14.3 (необходимое условие убывания функции). Пусть функция 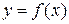 непрерывна на отрезке
непрерывна на отрезке 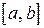 . Для того, чтобы она была всюду убывающей на этом отрезке необходимо, чтобы ее первая производная
. Для того, чтобы она была всюду убывающей на этом отрезке необходимо, чтобы ее первая производная 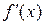 была всюду неположительна, т.е.
была всюду неположительна, т.е. 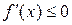 .
.
Теорема 14.4 (достаточное условие убывания функции). Пусть функция 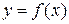 дифференцируема на отрезке
дифференцируема на отрезке 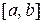 и ее производная
и ее производная 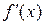 всюду отрицательна, т.е.
всюду отрицательна, т.е. 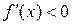 . Тогда функция
. Тогда функция  будет всюду убывающей.
будет всюду убывающей.
Символически это записать следующим образом:
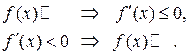
Напомним, что функция только возрастающая или только убывающая называются монотонными и термин «интервалы возрастания - убывания» – заменятся термином «интервал монотонности».
А теперь, вооруженные признаками для определения интервалов монотонности, а также теоремой Ферма для экстремумов, дадим признаки существования максимума и минимума функции для практического их применения.
14.5. Точки экстремума. Необходимые и достаточные условия
Определение 14.3. Точки, отделяющие интервал возрастания непрерывной функции от интервала убывания (или наоборот) называются экстремумами функции.
В зависимости от того, какие интервалы (возрастания или убывания) находятся слева и справа от экстремальной точки, их называют точками локального максимума или минимума, потому что значение функции в этих точках будут наибольшими или наименьшими только для некоторой их окрестности. Экстремальные точки всегда интересны, ведь они являются точками наивысшего подъема или падения, пусть даже и местного значения.
По теореме Ферма, рассмотренной в лекции 13, производная в этих точках равна нулю, либо не существует. Но как показывают контрпримеры, например функции для 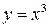 равенство нулю производной в точке
равенство нулю производной в точке 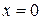 не гарантирует наличия экстремума – обратная теорема не всегда верна. И смотреть значения функции слева и справа от экстремумов тоже задача хоть и интересная, но иногда затруднительная. Например, как найти значения функции
не гарантирует наличия экстремума – обратная теорема не всегда верна. И смотреть значения функции слева и справа от экстремумов тоже задача хоть и интересная, но иногда затруднительная. Например, как найти значения функции 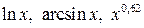 и др. функций, не имея под рукой хорошего калькулятора? Поэтому для нахождения точек экстремумов воспользуемся определением 14.3 и найдем простые, гарантированные признаки, позволяющие определять, как будет вести себя функция вблизи минимума или максимума – возрастать или убывать.
и др. функций, не имея под рукой хорошего калькулятора? Поэтому для нахождения точек экстремумов воспользуемся определением 14.3 и найдем простые, гарантированные признаки, позволяющие определять, как будет вести себя функция вблизи минимума или максимума – возрастать или убывать.
Теорема 14.5 (необходимое и достаточные условия максимума). Пусть функция 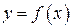 дифференцируема на отрезке
дифференцируема на отрезке 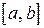 . Для того, чтобы функция в точке
. Для того, чтобы функция в точке 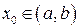 функция имела максимум необходимо, чтобы производная в этой точке равнялась
функция имела максимум необходимо, чтобы производная в этой точке равнялась 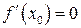 (или не существовала) и достаточно, чтобы
(или не существовала) и достаточно, чтобы 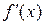 меняла свой знак с (+) на (–) при переходе через
меняла свой знак с (+) на (–) при переходе через  слева направо.
слева направо.
Необходимость следует из теоремы Ферма. Если  – точка максимума, то
– точка максимума, то 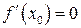 (или не существует).
(или не существует).
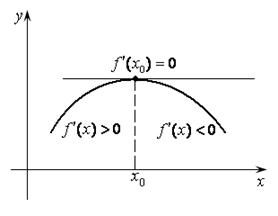
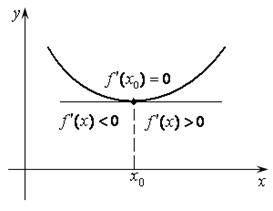
Рис. 14.4 Рис. 14.5
Достаточность диктуется определением максимума, как точки, отделяющей интервал возрастания от интервала убывания. Слева от  функция возрастает, следовательно, ее производная
функция возрастает, следовательно, ее производная 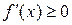 ; справа убывает и
; справа убывает и 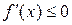 , т. е. меняет свой знак в точке
, т. е. меняет свой знак в точке  . Значит в точке
. Значит в точке  функция имеет максимум.
функция имеет максимум.
Аналогично вводится признак существования минимума функции.
Теорема 14.6 (необходимое и достаточные условия минимума). Пусть функция 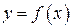 дифференцируема на отрезке
дифференцируема на отрезке 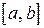 . Для того, чтобы функция в точке
. Для того, чтобы функция в точке 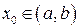 функция имела минимум необходимо, чтобы производная в этой точке равнялась
функция имела минимум необходимо, чтобы производная в этой точке равнялась 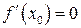 и достаточно, чтобы
и достаточно, чтобы 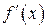 меняла свой знак с (–) на (+) при переходе через
меняла свой знак с (–) на (+) при переходе через  слева направо (рис. 14.5).
слева направо (рис. 14.5).
Таким образом, порядок действия нахождения экстремумов функции таков:
1. Находим 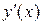 и решаем уравнение
и решаем уравнение 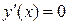 . К корням этого уравнения добавляем точки, в которых производная не существует. Все эти точки являются точками подозрительными на экстремум (критические точки).
. К корням этого уравнения добавляем точки, в которых производная не существует. Все эти точки являются точками подозрительными на экстремум (критические точки).
2. Определяем знаки 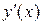 вблизи критических точек на всех интервалах непрерывности.
вблизи критических точек на всех интервалах непрерывности.
3. Делаем выводы о наличии экстремумов и интервалов возрастания и убывания.
4. Находим ординаты экстремальных точек 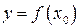 , где
, где  – экстремум.
– экстремум.
Обычно все значения знаков 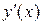 сводятся в таблицу (школьный прием) и делаются соответствующие выводы. Не будем ломать стереотип. Добавим только, что исследования необходимо проводить на всех интервалах непрерывности.
сводятся в таблицу (школьный прием) и делаются соответствующие выводы. Не будем ломать стереотип. Добавим только, что исследования необходимо проводить на всех интервалах непрерывности.
Пример 14.1. Определить экстремумы функций:
1) 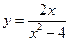 , 2)
, 2) 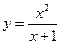 .
.
Решение. 1) С первой функцией мы уже знакомы и знаем, что ее ОДЗ являются интервалы 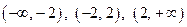 . Найдем
. Найдем
 .
.
а) 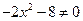 , т. к.
, т. к. 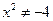 , поэтому экстремумов нет.
, поэтому экстремумов нет. 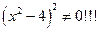
б) определим знак  на каждом из интервалов. Поскольку
на каждом из интервалов. Поскольку 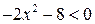 для любых
для любых 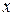 , то знак
, то знак  будет всегда отрицательным. То есть на всех интервалах непрерывности наша функция будет убывать, что и демонстрирует рис. 14.2.
будет всегда отрицательным. То есть на всех интервалах непрерывности наша функция будет убывать, что и демонстрирует рис. 14.2.
2) Исследуем вторую функцию по плану.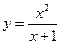 ,
, 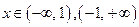 .
.
а) 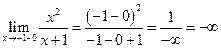 ,
, 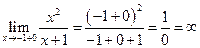 .
.
б) Функция общего вида, т.к. 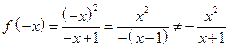 .
.
в) корни функции: 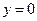 , если
, если 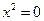 , т.е.
, т.е. 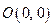 – корень. Точки пересечения с осью OY:
– корень. Точки пересечения с осью OY: 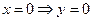 точка
точка 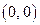 .
.
г) 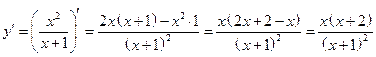 .
.
 , если
, если 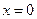 и
и 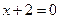 , т.е.
, т.е. 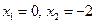 .
.
Составим таблицу знаков  .
.
| x | 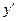 знак знак
| Вывод | 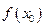
|

| + | возрастает | |
| –2 | максимум | 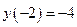
| |
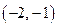
| – | убывает | |
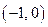
| – | убывает | |
| минимум | 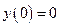
| ||
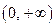
| + | возрастает |
Строим схематичный график (рис. 14.6.).
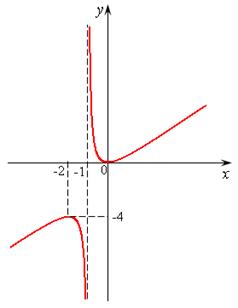
Рис. 14.6
Вот видите, здесь максимальная точка ниже минимальной, поэтому их и не называют наибольшим и наименьшим значениями функции.
14.6. Выпуклость – вогнутость формы графика. Точки перегиба
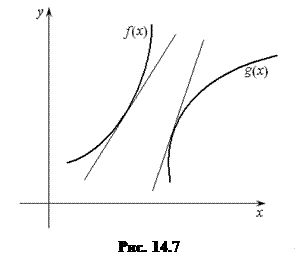 Посмотрите на графики функций
Посмотрите на графики функций 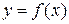 и
и 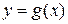 на рис. 14.7. Они обе возрастают, но характер их возрастания различный:
на рис. 14.7. Они обе возрастают, но характер их возрастания различный:  сначала медлит, а потом резко взлетает вверх,
сначала медлит, а потом резко взлетает вверх, 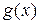 – наоборот: сначала взлетает, а потом ее скорость убывает. Различаются графики и по форме. Первый является вогнутым, второй – выпуклым, и это наблюдение связано с интуитивным наблюдением подобных кривых.
– наоборот: сначала взлетает, а потом ее скорость убывает. Различаются графики и по форме. Первый является вогнутым, второй – выпуклым, и это наблюдение связано с интуитивным наблюдением подобных кривых.
Дадим более строгое математическое определение вогнутости и выпуклости формы графика, а затем найдем признаки, по которым будем судить о наличии этих характеристик.
Определение 14.4. График дифференцируемой функции 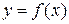 называется выпуклым на интервале
называется выпуклым на интервале  , если он расположен ниже любой своей касательной на этом интервале.
, если он расположен ниже любой своей касательной на этом интервале.
Определение 14.5. График дифференцируемой функции 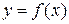 называется вогнутым на интервале
называется вогнутым на интервале  , если он расположен выше любой своей касательной на этом интервале.
, если он расположен выше любой своей касательной на этом интервале.
Определение 14.6. Точка графика непрерывной функции, отделяющая ее выпуклую часть от вогнутой, называется точкой перегиба (рис. 14.8).
Точки 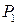 и
и 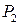 – точки перегиба.
– точки перегиба.
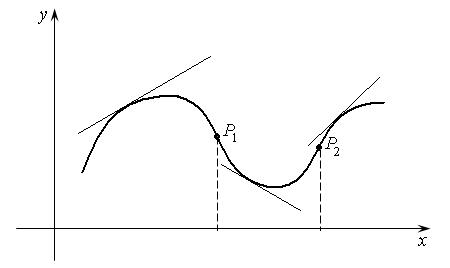
Рис. 14.8
Отметим, что условия выпуклости и вогнутости функции на некотором интервале, а также условия существования точек перегиба, формулируются точно также как и условия монотонности функции и существование точек экстремума, но для функции 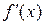 .
.
 Теорема 14.7. (необходимое условие выпуклости функции). Пусть
Теорема 14.7. (необходимое условие выпуклости функции). Пусть  непрерывна вместе со своими производными
непрерывна вместе со своими производными 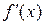 и
и 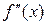 до второго порядка включительно на
до второго порядка включительно на  . Для того, чтобы ее график был выпуклым на интервале
. Для того, чтобы ее график был выпуклым на интервале  необходимо, чтобы
необходимо, чтобы 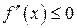 .
.
Доказательство.
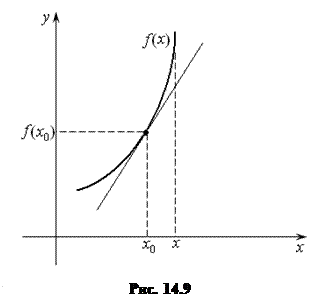
Для доказательства этого утверждения возьмем любую точку 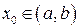 и составим уравнение касательной в этой точке, как уравнение прямой, проходящей через точку
и составим уравнение касательной в этой точке, как уравнение прямой, проходящей через точку 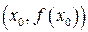 с угловым коэффициентом равным
с угловым коэффициентом равным  (рис. 14.9):
(рис. 14.9):
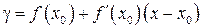 .
.
Возьмем вторую точку 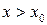 (для определенности, хотя может быть и меньше) и найдем разность ординат графика
(для определенности, хотя может быть и меньше) и найдем разность ординат графика 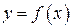 и касательной
и касательной 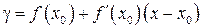 . Получаем
. Получаем
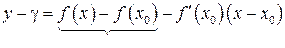 (14.1)
(14.1)
Применим к выделенной разности 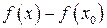 теорему Лагранжа:
теорему Лагранжа:
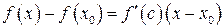 ,
,
где точка 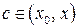 . Подставим получившееся выражение в (14.1):
. Подставим получившееся выражение в (14.1):
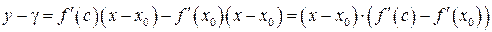 .
.
К последней разности еще раз применим теорему Лагранжа и получим:
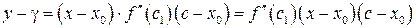 , (14.2)
, (14.2)
где  . Учтем, что
. Учтем, что 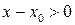 и
и 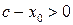 , тогда
, тогда 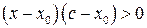 .
.
По условию теоремы дано: 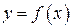 – выпуклый на
– выпуклый на 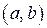 .
.
Требуется доказать: 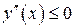 .
.
Так как график функции выпуклый, то любая его касательная лежит выше него, поэтому в равенстве (14.2) левая часть 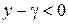 отрицательна. Следовательно, и правая часть должна быть отрицательной, а это возможно лишь при условии
отрицательна. Следовательно, и правая часть должна быть отрицательной, а это возможно лишь при условии 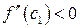 , а в пределе при
, а в пределе при  получим
получим 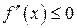 . Что и требовалось доказать.
. Что и требовалось доказать.
Теорема 14.8 (достаточное условие выпуклости функции). Пусть  непрерывна вместе со своими производными
непрерывна вместе со своими производными 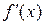 и
и 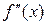 до второго порядка включительно на
до второго порядка включительно на  . Если
. Если 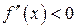 , то график функции
, то график функции  будет выпуклым на интервале
будет выпуклым на интервале  .
.
Доказательство.
Дано: 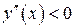
Доказать: 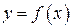 – выпукла.
– выпукла.
Теперь работаем с известной правой частью равенства (14.2). Она отрицательна, т. к. 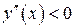 и
и 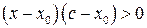 , поэтому и левая часть должна быть отрицательна, т. е
, поэтому и левая часть должна быть отрицательна, т. е 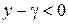 или
или 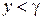 , что и говорит о выпуклости графика.
, что и говорит о выпуклости графика.
Запишем формулировки рассмотренных теорем символически следующим образом:
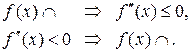
Необходимый и достаточный условия вогнутости графика формулируется аналогично.
Теорема 14.9 (необходимые условие вогнутости функции). Пусть  непрерывна вместе со своими производными
непрерывна вместе со своими производными 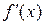 и
и 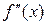 до второго порядка включительно на
до второго порядка включительно на  . Для того, чтобы ее график был вогнутым на интервале
. Для того, чтобы ее график был вогнутым на интервале  необходимо, чтобы
необходимо, чтобы 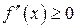 .
.
Теорема 14.10 (достаточное условие вогнутости функции). Пусть  непрерывна вместе со своими производными
непрерывна вместе со своими производными 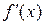 и
и 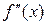 до второго порядка включительно на
до второго порядка включительно на  . Если
. Если 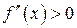 , то график функции
, то график функции  будет вогнутым на интервале
будет вогнутым на интервале  .
.
Символически эти теоремы можно записать так:
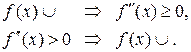
Доказательство этих теорем проведите самостоятельно.
Нахождение точек перегиба основано на следующей теореме.
Теорема 14.11 (необходимое и достаточные условия существования точек перегиба). Пусть функция 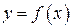 непрерывна вместе со своими производными
непрерывна вместе со своими производными 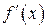 и
и 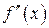 на
на 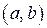 . Для того, чтобы точка
. Для того, чтобы точка  была точкой перегиба, необходимо, чтобы
была точкой перегиба, необходимо, чтобы 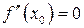 (или не существовала) и достаточно, чтобы
(или не существовала) и достаточно, чтобы 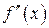 меняла свой знак при переходе через
меняла свой знак при переходе через  .
.
Этот признак сразу регламентирует порядок действий:
1. Находим 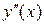 .
.
2. Решаем уравнение 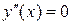 и находим точки, подозрительные на точки перегиба. Туда же входят и точки, где
и находим точки, подозрительные на точки перегиба. Туда же входят и точки, где 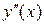 не существует.
не существует.
3. Смотрим знак 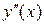 слева и справа от полученных точек и на всех интервалах непрерывности функции.
слева и справа от полученных точек и на всех интервалах непрерывности функции.
4. Делаем выводы об интервалах выпуклости, вогнутости и точек перегиба. Находим ординаты точек перегиба.
Как мы видим, порядок действий аналогичен порядку действий для определения интервалов возрастания, убывания функции и точек экстремумов.
Пример 14.2. Определить интервалы выпуклости – вогнутости и точки перегиба функции 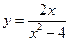 .
.
Решение: Область допустимых значений этой функции
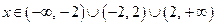 .
.
Первая производная этой функции была найдена на прошлой лекции:
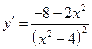 .
.
Поэтому продолжаем далее.
1. 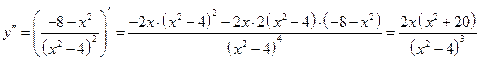 .
.
2. 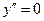 , если
, если 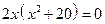 ,
, 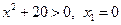 . Единственная точка, подозрительная на перегиб, это точка
. Единственная точка, подозрительная на перегиб, это точка 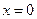 .
.
3. Рисуем таблицу знаков  с учетом интервалов непрерывности и сразу делаем выводы.
с учетом интервалов непрерывности и сразу делаем выводы.
| x | 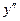 , знак , знак
| вывод | 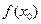
|

| – < 0 | выпуклый Ç | |
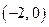
| + > 0 | вогнутый È | |
| точка перегиба | 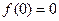
| ||
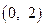
| – | выпуклый Ç | |
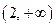
| + | вогнутый Ç |
Чертим график.
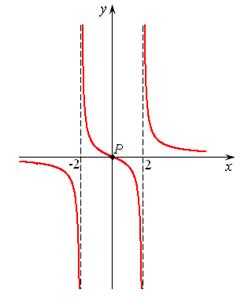
Рис. 14.10
Пример 14.3. Определить интервалы выпуклости – вогнутости и точки перегиба функции 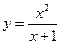 .
.
Решение: Область допустимых значений этой функции
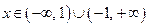
Первая производная этой функции также была найдена на прошлой лекции:
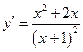 .
.
Продолжаем далее.
1. 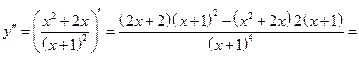
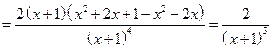 .
.
2. 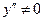 , точек перегиба нет, т.к. числитель этой дроби отличен от нуля. Поэтому определим знак
, точек перегиба нет, т.к. числитель этой дроби отличен от нуля. Поэтому определим знак 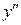 на интервалах непрерывности.
на интервалах непрерывности.
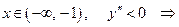 кривая выпукла,
кривая выпукла,
 ,
, 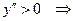 кривая вогнута.
кривая вогнута.
График этой функции был приведен на прошлой лекции (рис. 14.6).
14.7. Асимптоты функции
С понятием асимптоты, т. е. прямой, к которой стремятся точки графика функции 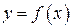 при неограниченном удалении от начала координат, мы знакомились на примере гиперболы (см. тему «Аналитическая геометрия»). Поскольку любая прямая в декартовой системе координат может быть либо параллельна осям координат, либо наклонена под произвольным углом
при неограниченном удалении от начала координат, мы знакомились на примере гиперболы (см. тему «Аналитическая геометрия»). Поскольку любая прямая в декартовой системе координат может быть либо параллельна осям координат, либо наклонена под произвольным углом 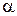 к оси
к оси  , то и асимптоты могут быть горизонтальными, вертикальными и наклонными (рис. 14.11).
, то и асимптоты могут быть горизонтальными, вертикальными и наклонными (рис. 14.11).
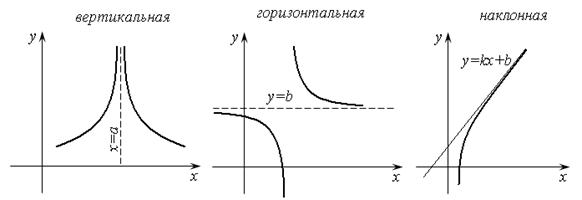
Рис. 14.11
Проще всего найти вертикальнуюасимптоту. Она, как правило, присутствует в точках разрыва 2-го рода, где один или оба односторонние предела не существуют, т. е. 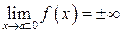 . Это точки, где знаменатель обращается в нуль или граничные точки области определения функции.
. Это точки, где знаменатель обращается в нуль или граничные точки области определения функции.
Например, функция 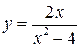 имеет 2 точки разрыва 2-го рода:
имеет 2 точки разрыва 2-го рода: 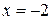 и
и 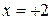 . Подробно ее поведение мы обсудили в примере 14.3. Односторонние пределы равны
. Подробно ее поведение мы обсудили в примере 14.3. Односторонние пределы равны 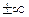 , поэтому делаем вывод, что прямые
, поэтому делаем вывод, что прямые 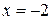 и
и 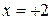 являются вертикальными асимптотами.
являются вертикальными асимптотами.
Функция 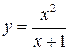 имеет одну точку бесконечного разрыва:
имеет одну точку бесконечного разрыва: 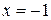 , поэтому прямая
, поэтому прямая 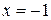 – вертикальная асимптота. Функция
– вертикальная асимптота. Функция 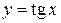 при
при 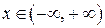 имеет множество точек разрыва 2-го рода
имеет множество точек разрыва 2-го рода 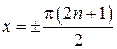 , где
, где 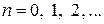 и, следовательно, столько же вертикальных асимптот. Вспомните график тангенсоиды, и вам все станет понятным.
и, следовательно, столько же вертикальных асимптот. Вспомните график тангенсоиды, и вам все станет понятным.
Функция 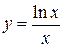 имеет одну точку, подозрительную на разрыв:
имеет одну точку, подозрительную на разрыв: 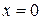 . В ней и знаменатель обращается в нуль и
. В ней и знаменатель обращается в нуль и 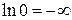 . То есть
. То есть  . Действительно прямая
. Действительно прямая 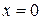 , т.е. ось
, т.е. ось 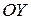 , будет левосторонней (располагающейся слева от графика) асимптотой (рис. 14.12).
, будет левосторонней (располагающейся слева от графика) асимптотой (рис. 14.12).
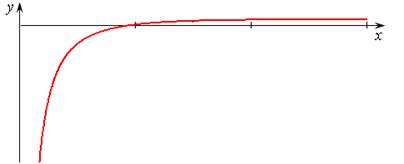
Рис. 14.12
Практически также просто определить наличие горизонтальнойасимптоты. Если функция 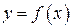 при
при  имеет предел, равный числу
имеет предел, равный числу 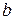 , то прямая
, то прямая 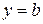 является горизонтальной асимптотой.
является горизонтальной асимптотой.
Например: функция 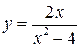 имеет горизонтальную асимптоту, т.к.
имеет горизонтальную асимптоту, т.к. 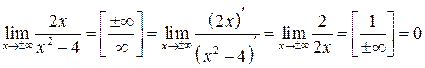 , т. е. при
, т. е. при 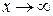 прямая
прямая 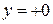 служит нижней горизонтальной асимптотой, график функции располагается выше оси
служит нижней горизонтальной асимптотой, график функции располагается выше оси  . Если
. Если 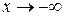 , то ось
, то ось  является верхней горизонтальной асимптотой, т.к.
является верхней горизонтальной асимптотой, т.к. 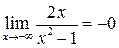 (рис. 15.4).
(рис. 15.4).
Функция 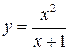 не имеет горизонтальной асимптоты, т. к.
не имеет горизонтальной асимптоты, т. к. 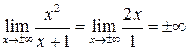 .
.
И, наконец, функция 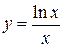 при
при 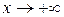 также имеет горизонтальную асимптоту
также имеет горизонтальную асимптоту 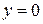 (верхнюю или нижнюю?).
(верхнюю или нижнюю?).
Определить характер стремления к своей асимптоте проще всего, найдя предел разности 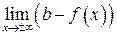 . Если он больше нуля, то асимптота проходит выше графика функции, меньше – ниже.
. Если он больше нуля, то асимптота проходит выше графика функции, меньше – ниже.
Именно этот прием – нахождения разности между точками, лежащими на прямой и графиком функции 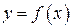 , – лежит в основе определения параметров наклонной асимптоты.
, – лежит в основе определения параметров наклонной асимптоты.
На рисунке 14.13 приведен график функции 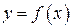 , имеющий наклонную асимптоту. Это значит, что разность
, имеющий наклонную асимптоту. Это значит, что разность 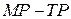 стремится к нулю при неограниченном удалении от начала координат, т. е. при
стремится к нулю при неограниченном удалении от начала координат, т. е. при 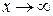 . Пусть уравнение асимптоты записано в виде
. Пусть уравнение асимптоты записано в виде 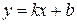 , функции
, функции 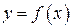 .
.
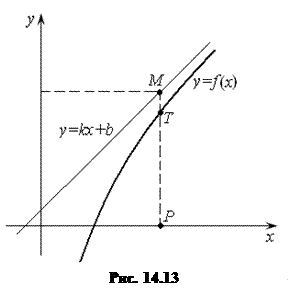 Найдем указанную разность значений
Найдем указанную разность значений 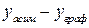 при одинаковых значениях аргумента
при одинаковых значениях аргумента 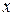 :
:
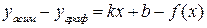 . (14.3)
. (14.3)
При 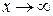 эта разность должна стремиться к нулю, т. е.
эта разность должна стремиться к нулю, т. е.
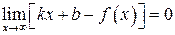 . (14.4)
. (14.4)
Преобразуем выражение, стоящее под знаком предела. Вынесем 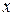 за скобки, получим:
за скобки, получим:
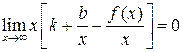 .
.
Для того, чтобы это произведение было равно нулю, необходимо чтобы хотя бы один сомножитель был равен нулю. Т.к. 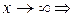 , то только
, то только 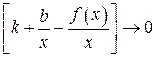 . Но
. Но 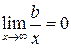 , поэтому остается
, поэтому остается 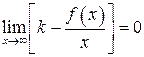 , откуда
, откуда
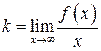 . (14.5)
. (14.5)
Вернемся к равенству (14.4). Найдем из него 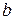 , помня, что предел постоянной равен самой постоянной:
, помня, что предел постоянной равен самой постоянной:
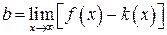 , (14.6),
, (14.6),
где  находится по формуле (14.5).
находится по формуле (14.5).
Если хотя бы один из этих пределов не существует – график функции 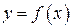 наклонной асимптоты не имеет. Очевидно, что по тем же формулам можно найти наклонные асимптоты и при
наклонной асимптоты не имеет. Очевидно, что по тем же формулам можно найти наклонные асимптоты и при 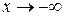 , причем случается, что они не совпадают.
, причем случается, что они не совпадают.
Пример 14.4. Определить, будет ли функция 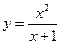 иметь наклонную асимптоту.
иметь наклонную асимптоту.
Решение: Воспользуемся формулами (14.5) и (14.6)
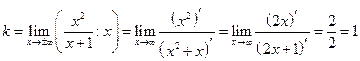 ,
,
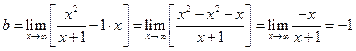 .
.
Таким образом, прямая 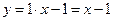 является наклонной асимптотой при
является наклонной асимптотой при 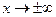 .
.
Для правильного построения графика функции и асимптоты найдем разность 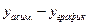 при
при 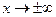 .
.
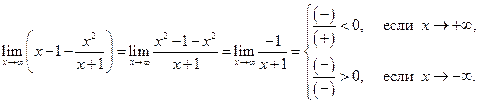
То есть, если 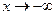 , то асимптота располагается выше графика функции, если
, то асимптота располагается выше графика функции, если 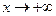 , то ниже.
, то ниже.
Строим график, учитывая все предыдущие исследования.
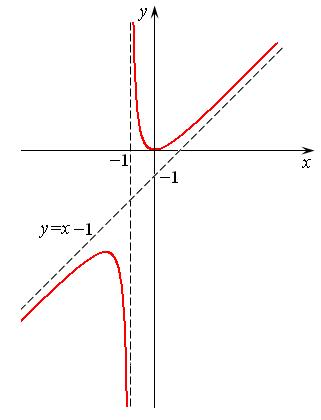
Рис. 14.14
14.8. Пример исследования функции
Для закрепление этого большого материала проведем полное исследование функции по плану, означенному в начале лекции:
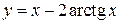 .
.
1. Область определения функции: 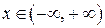 , точек разрыва нет.
, точек разрыва нет.
2. Симметрия: 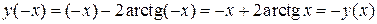 , т. е. данная функция нечетная, проходит через точку
, т. е. данная функция нечетная, проходит через точку 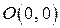 ,
, 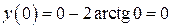 и имеет корни, которые можно найти решив уравнение,
и имеет корни, которые можно найти решив уравнение, 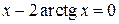 . Решим это уравнение графически
. Решим это уравнение графически 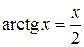 . Построим график функции
. Построим график функции 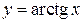 и
и  . Если они пересекутся – то исходная функция имеет корни. График функции
. Если они пересекутся – то исходная функция имеет корни. График функции 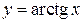 получается симметричным отражением графика
получается симметричным отражением графика 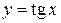 относительно прямой
относительно прямой 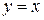 . Прямую
. Прямую  построим по точкам.
построим по точкам.
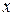
| 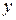
|
| 0,5 |
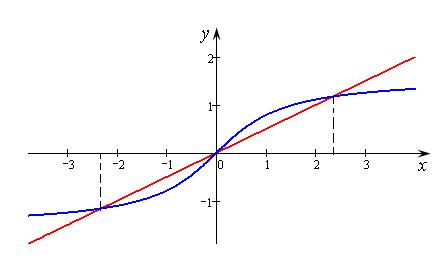
Рис. 14.15
Как видно из рис. 14.15 эти два графика пересекаются в точках 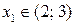 и
и 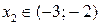 , то есть корни функции лежат в этих интервалах. Более точно найти корни можно при помощи метода половинного деления (см. лекцию 10).
, то есть корни функции лежат в этих интервалах. Более точно найти корни можно при помощи метода половинного деления (см. лекцию 10).
3. Экстремумы, интервалы возрастания – убывания.
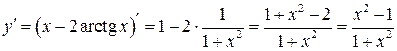 .
.
Тогда 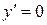 , если
, если 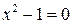 , т.е. если
, т.е. если 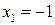 и
и 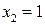 . Определим знак
. Определим знак  на каждом из интервалов
на каждом из интервалов 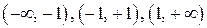 . Данные сведем в таблицу
. Данные сведем в таблицу
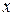 , интервал , интервал
|  , знак , знак
| вывод | 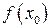
|
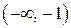
| + | возрастает | |

| максимум | 0,57 | |

| – | убывает | |
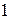
| минимум | –0,57 | |
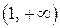
| + | возрастает |
Найдем значения исходной функции в экстремальных точках и начертим первый «прибросочный» график (рис. 14.16).
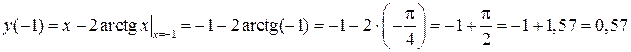 ,
,
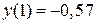 в силу симметрии.
в силу симметрии.
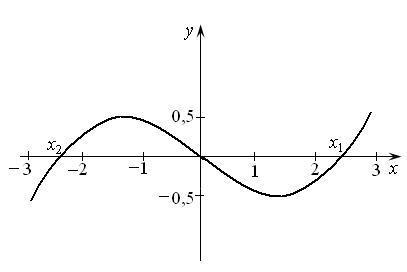
Рис. 14.16
4. Точки перегиба, интервалы выпуклости вогнутости.
Найдем
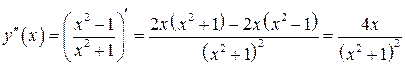 .
.
Тогда 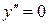 , если
, если 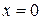 .
.
Составим таблицу знаков для 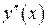 , которая подтверждает наш рис. 15.9.
, которая подтверждает наш рис. 15.9.
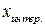
| 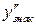
| Вывод | 
|
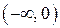
| – | выпуклая | |
| точка перегиба | |||
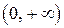
| – | вогнутая |
5. Найдем наклонные асимптоты функции, так как ни вертикальной ни горизонтальной она иметь не может (почему?), причем учтем, что их в силу симметрии будет две. Итак, найдем  и
и 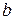 для уравнения
для уравнения 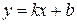 .
.
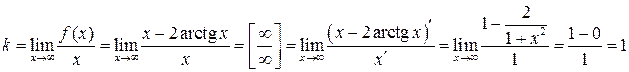 ,
,
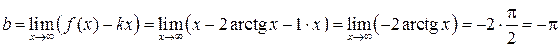 .
.
Здесь мы учли, что 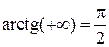 . То есть прямая
. То есть прямая 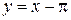 является правосторонней наклонной асимптотой
является правосторонней наклонной асимптотой 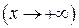 .
.
Если 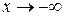 , то коэффициент
, то коэффициент  не изменится, а
не изменится, а 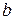 станет равным
станет равным 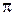 , потому что
, потому что 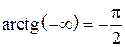 . Левосторонняя асимптота имеет вид
. Левосторонняя асимптота имеет вид 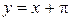 . Начертим общий график (рис. 14.17).
. Начертим общий график (рис. 14.17).
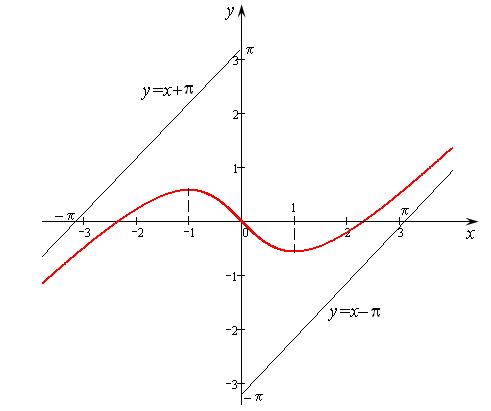
Рис. 14.17
14.9. Заключение
На этом мы закончим тему «Исследование функции методами дифференциального исчисления». Этот материал вам необходим для решения соответствующей задачи контрольного задания.
Следующий материал поможет вам в практической работе при исследовании функций, заданных таблично или графически.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 3820; Нарушение авторских прав?; Мы поможем в написании вашей работы!