Решение. Откуда получим две критические точки и

1.Найдем критические точки:

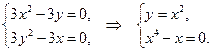
Откуда получим две критические точк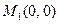и и .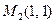

2. Производные второго порядка:

, , .

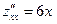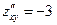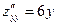3. В точке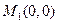

, , , .

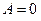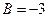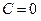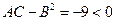Следовательно в этой точке минимакс.

4. В точке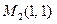

, , , .

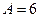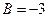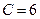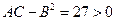Следовательно в этой точке функция имеет минимум, так как .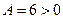

5. , .

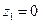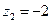17.4. Наибольшее и наименьшее значение функции
в замкнутой области

Для того чтобы найти наименьшее и наибольшее значения функции 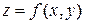в ограниченной области D, следует найти значения функции в экстремальных точках и на границах области. Наибольшее и наименьшее из них являются соответственно наибольшим и наименьшим значениями функции 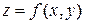в области D. При отыскании этих значений на границе области следует в уравнение 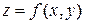подставить уравнение границы, разрешенное относительно одной переменной и рассматривать вопрос как для функции одной переменной. Покажем это на примере.

Пример 17.6. Найти наибольшее и наименьшее значение функции

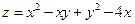
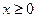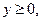
в замкнутой области D, заданной системой неравенств , 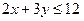. Сделать чертеж.

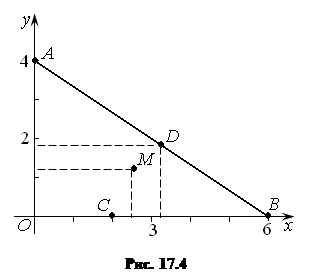Решение. Сделаем чертеж области D. Она ограничена сторонами треугольника АОВ, причем уравнение АВ: 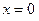, уравнение ОВ: 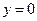, уравнение АВ: 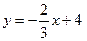(рис. 17.4).

Дальнейшее решение проведем по плану:

1. Найдем критические точки, в которых частные производные равны нулю:

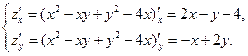
Приравняем их нулю: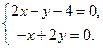

Решив эту систему, получим 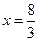, 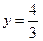. Точка М (8/3, 4/3) принадлежит области D.

2. Определим, будет ли в этой точке экстремум, для чего воспользуемся достаточным условием (17.1) предыдущего пункта:

,

.

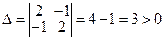Так как 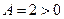, следовательно, в точке М – min.

.

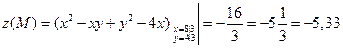3. Найдем наименьшее и наибольшее значение функции z на границах области:

а) на границе ОА: 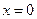, тогда функция 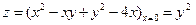, где .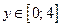

Эта функция монотонно возрастает на данном отрезке, и ее наименьшее и наибольшее значения находятся на концах отрезка в точках А и О. , .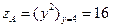

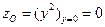б) на границе ОВ: 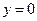, поэтому 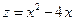, где 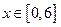. Найдем экстремум и значения функции на концах отрезка в т. О (0,0) и точка В (6,0).

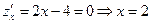
– это точка минимума точке С, т.к. парабола с поднятыми вверх ветками имеет только минимум.

, , .

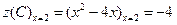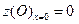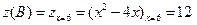в) на границе АВ: 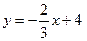. Запишем функцию z с учетом уравнения границы:

и .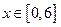

Найдем только экстремум, так как значения функции в точках А и В были найдены выше.

.

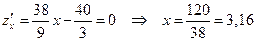Это тоже точка минимума, назовем ее точкой D. Найдем значение функции в этой точке:

.

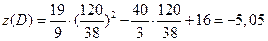г) Запишем и сравним значения функции, во всех экстремальных и граничных точках области:

, , , , , .

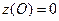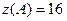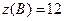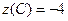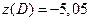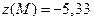Очевидно, что наибольшее значение функция принимает в граничной точке области А и наименьшее – во внутренней точке минимума М.

Таким образом, нахождение наибольшего и наименьшего значения функции в замкнутой области свелось к функции одной переменной, с чем мы уже встречались в теме «Экстремумы функции одной переменной».

Если требуется определить наименьшее и наибольшее значение функции многих переменных, которые связаны друг с другом какими-то добавочными условиями, то эта задача так и называется задачей на условные экстремумы. Она выходит за рамки рассматриваемого курса. Ее можно найти в рекомендуемой литературе.

17.5. Подбор параметров для эмпирических формул простейшего
вида по методу наименьших квадратов

Рассматривая функции одной и многих переменных по способам их задания, мы всегда переходили от одного способа к другому по цепочке
формула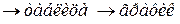, причем взаимный переход двух последних способов осуществлялся достаточно просто. Составление уравнения, связывающего две переменные величины, полученные при проведении опытов, натолкнулось на трудности двух видов.

1. Определение вида аппроксимирующей (приближенной) функции – линейной, степенной, гиперболической и т.д. Ее можно было решить из логики процесса: из теоретических соображений или на основании характера расположения точек, соответствующих экспериментальным данным.

2. Определение коэффициентов выбранной зависимости, чтобы она в каком-то смысле наилучшим образом описывала рассматриваемый процесс.

Для решения второй задачи разработаны различные методы корреляционного и дисперсионного анализа, в основе которых лежат два требования, предъявляемых к выбранной функции:

3. Сумма отклонений эмпирических данных от расчетных должна быть равна нулю:

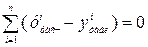. (17.2)

Это требование было необходимым, но недостаточным для того, чтобы определить коэффициенты искомой функции. Поэтому выдвинули второе требование

4. Сумма квадратов отклонений эмпирических данных от расчетных должна быть наименьшей:

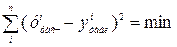. (17.3)

Отсюда название метода – метод наименьших квадратов. Покажем его действие на примере.

Пусть в результате эксперимента получено n значений функции у при соответствующих значения х. Результаты записаны в таблицу.

Таблица 17.1

			…
			…

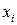
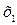
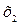
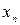
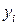
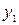
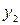
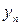
Требуется построить кривую, наилучшим образом описывающую эти данные. Она может быть любого вида – прямая, гипербола и т.д. Остановимся на простейшем – прямой, уравнение которой запишем в виде .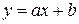

Рассмотрим сумму квадратов разностей значений по формуле (17.2):

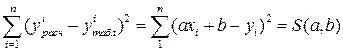. (17.3)

Подберем параметры а и b так, чтобы эта сумма имела наименьшее значение – то есть решим задачу из п. 17.3. На основании теоремы 17.1 следует, что частные производные функции S (a, b) по параметрам а и b должны быть равны нулю. Учтем, что функция S (a, b) сложная, поэтому сначала берем производную от квадрата, а потом от суммы:

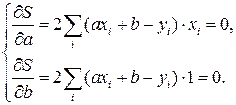(17.4)

Сократим оба уравнения на 2 и запишем их в виде системы уравнений.

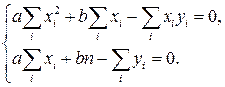(17.5)

Эта система всегда имеет решение. Для удобства ее решения в таблицу опытных данных добавим столбцы 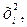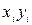, , 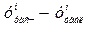а также строку для записи соответствующих сумм.

Пример 17.7. В результате опыта получены следующие данные:

№
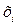
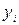
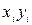
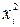
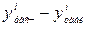
	0,25	2,57	0,6425	0,0625	0,0049
	0,37	2,31	0,8547	0,1369	–0,0116
	0,44	2,12	0,9328	0,1936	0,0171
	0,55	1,92	1,0560	0,3025	–0,0362
	0,60	1,75	1,050	0,3600	0,0186
	0,62	1,71	1,0602	0,3844	0,0125
	0,68	1,60	1,088	0,4624	–0,0157
	0,70	1,51	1,0570	0,4900	0,0282
	0,73	1,50	1,0950	0,5329	–0,0237
	0,75	1,41	1,0575	0,5625	0,013
Сумма	5,69	18,4	9,8937	3,4877	0,0001

Для нахождения коэффициентов а и b подставим в систему (17.5) найденные значения сумм и получим следующее:

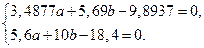
Решим ее любым способом и найдем значения

а = –2,3038 и b = 3,1508.

Таким образом, искомое уравнение связи между у и х будет иметь вид

.

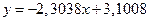Построим полученную прямую (рис. 17.5).

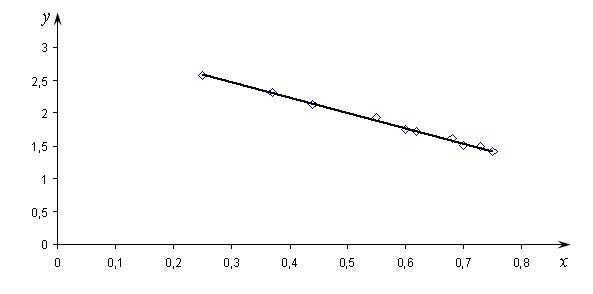
Рис. 17.5

Для проверки правильности подобранных коэффициентов составляем разности между расчетными и табличными значениями у. Покажем, как это делается.

Если х = 0,25, то

, .

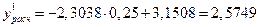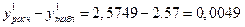Если х = 0,37, то

,

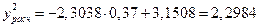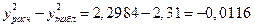
и т.д.

Суммарная ошибка отлична от нуля в четвертом знаке после запятой, а исходные данные имели два знака, поэтому в условиях нашего опыта можно считать, что ошибка приближения практически равна нулю.

Если за аппроксимирующую функцию взят трехчлен второй степени

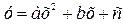, (17.6)

то выражение (17.3) запишется в виде

, (17.7)

а соответствующая система (17.4) будет иметь три уравнения с тремя неизвестными a,b,c

Сейчас подбор вида и коэффициентов соответствующей функциональной зависимости можно осуществить на компьютере. В основе практически всех программ и «Exсel» и «Статистика» лежит проверенный метод наименьших квадратов.

На этом мы заканчиваем тему «Функции многих переменных». Последняя лекция проиллюстрировала всеобщий закон развития: количество рождает новое качество. Две независимые переменные привели две частных производных первого порядка и четыре – второго. Появились чистые и смешанные производные высших порядков, производная по направлению и градиент. К привычным со школы минимуму и максимуму присоединился минимакс. О, сколько нам открытий чудных …. И это – правда. Готовит.

Дата добавления: 2014-01-04