Потоковые методы

Previously we developed our differencing schemes by considering Taylor series expansions about a point. In this section, we will develop an alternative approach for deriving difference equations that is similar to the way we developed the original conservation equations. This approach will become useful for deriving the upwind and mpdata schemes described below.

The control volume approach divides up space into a number of control volumes of width ∆x surrounding each node i.e. and then considers the integral form of the conservation equations

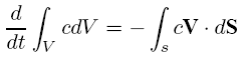
If we now consider that the value of c at the center node of volume j is representative of the average value of the control volume, then we can replace the first integral by c_j∆x. The second integral is the surface integral of the flux and is exactly

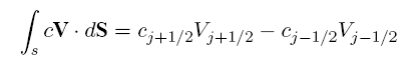
which is just the difference between the flux at the boundaries F_j+1/2 and F_j−1/2.

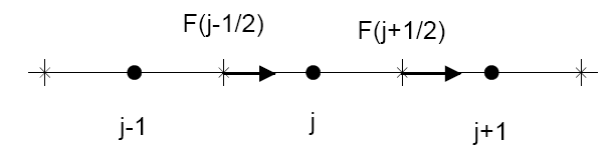
Figure: A simple staggered grid used to define the control volume approach. Dots denote nodes where average values of the control volume are stored. X’s mark control volume boundaries at half grid points.

If we assume that we can interpolate linearly between nodes then c_j+1/2 = (c_j+1 +c_j)/2. If we use a centered time step for the time derivative then the flux conservative centered approximation to

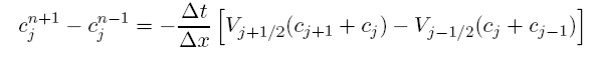
or if V is constant Eq. (5.5.13) reduces identically to the staggered leapfrog scheme. By using higher order interpolations for the fluxes at the boundaries additional differencing schemes are readily derived. The principal utility of this sort of differencing scheme is that it is automatically flux conservative as by symmetry what leaves one box must enter the next. The following section will develop a slightly different approach to choosing the fluxes by the direction of transport.

Численная схема против потока (донорская ячейка)

The fundamental behavior of transport equations such as (5.5.13) is that every particle will travel at its own velocity independent of neighboring particles (remember the characteristics), thus physically it might seem more correct to say that if the flux is moving from cell j − 1 to cell j the incoming flux should only depend on the concentration upstream. i.e. for the fluxes shown in Fig. 5.6 the upwind differencing for the flux at point j − 1/2 should be

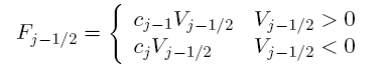
with a similar equation for F_j+1/2. Thus the concentration of the incoming flux is determined by the concentration of the donor cell and thus the name. As a note, the donor cell selection can be coded up without an if statement by using the following trick

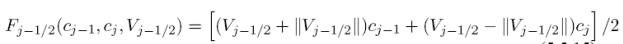
Simple upwind donor-cell schemes are stable as long as the Courant condition is met. Unfortunately they are only first order schemes in ∆t and ∆x and thus the truncation error is second order producing large numerical diffusion (it is this diffusion which stabilizes the scheme). If we do a Hirt’s style stability analysis for constant velocities, we find that the actual equations being solved to second order

are

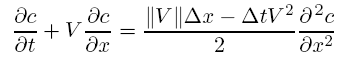
or in terms of the Courant number

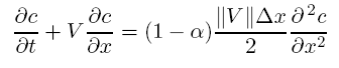
Thus as long as α < 1 this scheme will have positive diffusion and be stable. Unfortunately, any initial feature won’t last very long with this much diffusion. Figure (5.7) shows the effects of this scheme on a long run with a gaussian initial condition. The boundary conditions for this problem are periodic (wraparound) and thus every new curve marks another pass around the grid (i.e. after t = 10 the peak should return to its original position). A staggered leapfrog solution of this problem would be almost indistinguishable from a single gaussian.

Улучшенная схема против потока (схема Смоляркевича)

Donor cell methods in their simplest form are just too diffusive to be used with any confidence for long runs. However a useful modification of this scheme by Smolarkiewicz [2] provides some useful corrections that remove much of the numerical diffusion. The basic idea is that an upwind scheme (with non-constant velocities) is actual solving an advection-diffusion equation of the form

,

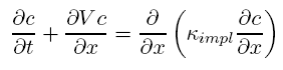where

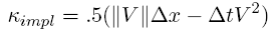
is the implicit numerical diffusivity. One obvious approach (to quote Smolarkiewicz) “is to make the advection step using a [donor cell method] and then reverse the effect of the diffusion equation

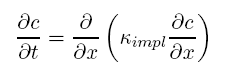
in the next corrective step.

The problem is that the diffusion process and the equation that describes it are irreversible. But it is not true that the solution of the diffusion equation cannot be reversed in time. Just as a film showing the diffusion process may be reversed in time, the equivalent numerical trick may be found to produce the same effect. It is enough to notice that (5.5.20) may be written in the form

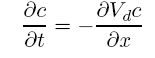
where

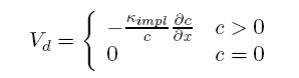
[this scheme assumes that the advected quantity is always positive]. Here V_d will be referred to as the “diffusion velocity.” Now, defining an “anti-diffusion velocity”

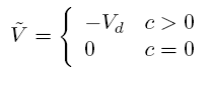
the reversal in time of the diffusion equation may be simulated by the advection equation (5.5.21) with an anti-diffusion velocity ˜ V. Based on these concepts, the following advection scheme is suggested... ”. If we define the donor cell algorithm as

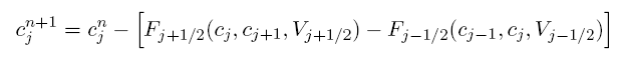
where F is given by (5.5.15) then the mpdata algorithm is to first take a trial donorcell step

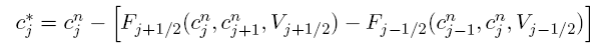
then take a corrective step using the new values and the anti-diffusion velocity ˜ V, i.e.

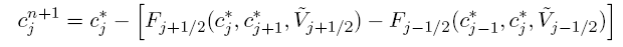
This scheme is actually iterative and could be repeated ad nauseum although in practice, any more than 2 additional corrections (3 iterations) is a waste of time. Figure 5.8a,b shows the results of the mpdata algorithm for 1 and 2 corrective steps. Comparison to the standard upwind scheme (which is just one pass of mpdata) in Fig. 5.7 shows the remarkable improvement this approach can deliver.

In addition to the anti-diffusive correction, the more recent versions of mpdata also continue the analysis to third order truncation terms and offer an option for an anti-dispersive correction as well. The routine provided in the problem set (upmpdata1p.f) implements both the 2nd and 3rd order corrections. This scheme is comparable and computationally cheaper than the most sophisticated flux corrected transport schemes, however, it is still much more expensive than the simple staggered-leapfrog scheme. Moreover, given it’s computational expense and the fact that it still has a stability requirement given by the courant condition, it is difficult to whole-heartedly recommend this scheme. The principal difficulty is that it seems to be taking most of it’s time correcting a really quite poor advection scheme and it would make more sense to find a scheme that better mimics the underlying physics. Fortunately, there are the semi-lagrangian schemes.

Полулагранжевая схема

Модельные уравнения чаще всего выражаются в Эйлеровском (Eulerian) подходе, т.е в фиксированных по отношению к пространству координатах. Преимущества такого подхода заключаются в том, что изменчивость переменных, которые описывают состояние исследуемой жидкости, описывается в фиксированной точке пространства. Лагранжев (Lagrangian) подход отличается от Эйлеровского тем, что рассматривается объем жидкости, перемещающийся вместе с потоком. Различие между двумя подходами можно заметить по форме второго закона Ньютона:

,

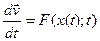где 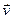- скорость объема воздуха, а 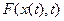- результирующая всех сил, действующих на единицу массы объема воздуха. Объем движется по траектории в пространстве, поэтому x зависит от времени t. В формулировке же Эйлера 2-й закон Ньютона имеет вид:

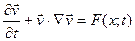
С одной стороны, вид уравнения для Лагранжева подхода проще, а с другой стороны, чаще используется Эйлеров подход, т.к. он позволяет выражать скорость перемещения объема и силы, действующие на него, как функции пространства и определять их в каждой точке. При этом координата x не зависит более от времени t. В Лагранжевом подходе необходимо знать всю траекторию частицы, кроме того, более сложным образом описывается связь между траекториями.

Эйлеров Подход может быть реализован в абсолютной или относительной системе координат. В абсолютной декартовой (прямоугольной) системе координат центр находится в центре Земли, ось z направлена вдоль оси вращения Земли, а оси x и y - неподвижно относительно звезд. Относительные системы координат могут быть локальными и глобальными. В локальных системах координат пренебрегают кривизной Земли и считают систему координат Декартовой (прямоугольной). В локальных координатах строят модели загрязнений городов, распространения выбросов, облачные модели.

As the previous sections show, there are really two principal difficulties with Eulerian grid-based schemes. First, they introduce unwanted length scales into the problem because information can propagate from grid-point to grid-point even though the underlying transport equations has no information transfer between characteristics. Usually, this only affects wavelengths that are comparable to the grid-spacing (which are not resolved anyway), however over time these effects can lead to numerical diffusion or dispersion depending on the structure of the truncation error. The second problem with Eulerian schemes is that the Courant condition couples the time step to the spatial resolution, thus to increase the number of grid points by two, increases the total run time by four because we have to take twice as many steps to satisfy the Courant condition. For 1-D problems, this is not really a problem, however in 3-D, doubling the grid leads to a factor of 16 increase in time. Clearly, in a perfect world we would have an advection scheme that is true to the underlying particle-like physics, has no obvious Courant condition yet still gives us regularly gridded output. Normally I would say we were crazy but the Semi-Lagrangian schemes promise just that. They are somewhat more difficult to code and they are not inherently conservative, however, for certain classes of problems they more than make up for it in speed and accuracy. Staniforth and Cote [3] provide a useful overview of these techniques and Figure 5.9 illustrates the basic algorithm.

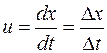
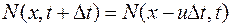
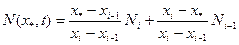
Нужно найти среднее значение скорости перемещения объема массы и принять, что это среднее значение является постоянным в течение шага времени

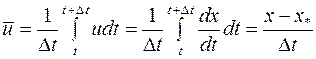
Given some point сⁿ⁺¹_j we know that there is some particle with concentration ˜c at step n that has a trajectory (or characteristic) that will pass through our grid point c_n+1 j in time ∆t.

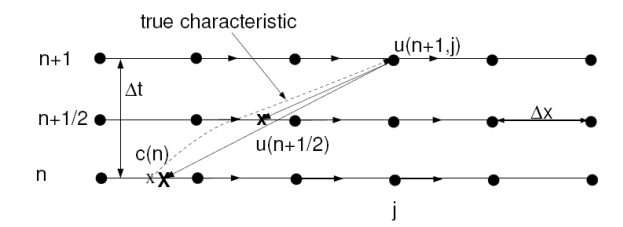
Figure: Schematic description of the semi-lagrangian advection scheme. x marks the point at time n that lies on the true characteristic that will pass through our grid-point j in time ∆t. X is the best approximation for this point found by taking a backwards mid-point step from the future time; To get the concentration at this point we must use some interpolation scheme. If there are no source terms, however, concentration remains constant along a characteristic and cⁿ⁺¹_j = ˜cⁿ. x is the position at time ∆t/2 where we calculate the mid-point velocity.

The problem is to find this point because the solution to Eq. (5.2.2) is that the concentration remains constant along characteristics i.e. cⁿ⁺¹_j = ˜c. The important feature of transport equations, however, is that they can be run backwards in time stably, thus rather than guessing at an old point and moving it forward, we will start at our new point (j, n + 1) and use our ODE techniques to shoot backwards in time. Fig. 5.9 (and 5.8d) uses a simple mid-point scheme. The basic algorithm can be summarized as follows.

For each point j

1. given the velocity at our future point uⁿ⁺¹ _j, find the fractional grid-point x with coordinate ˜j = j − (∆tuⁿ⁺¹_j)/(2∆x) (i.e. take an Euler step back for half a time step).

2. Using some interpolation scheme find the velocity at the half-time step u^n+1/2 _˜j

3. repeat the step nvit times using the new velocity to iterate and find a better approximation to u^n+1/2 _˜j

.4. When you’re happy use the centered velocity to find the fractional grid-point X with coordinate ˜j₀ = j − (∆tu^n+1/2_˜j)/ ∆x)

5. Using another interpolation scheme, find the concentration at point ˜j₀ and copy into cⁿ⁺¹_j

This formulation should be treated as a recipe that is easily varied. For example, here we have used an iterative mid-point scheme, to find the point at time t − ∆t, however, with only bit more work, a 4th order fixed step Runge-Kutta scheme could also be easily employed.

Дата добавления: 2014-01-04