Анализ устойчивости численных схем

Hirt’s method can be thought of as reverse Taylor series differencing where we start with finite difference approximation and come up with the actual continuous partial differential equation that is being solved. Given the FTCS scheme in (5.3.21) we first expand each of the terms in a Taylor series about each grid point e.g. we can express the point cⁿ⁺¹ _j as

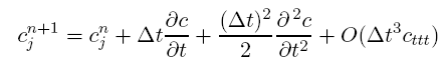
likewise for the spatial points cⁿ_j±1

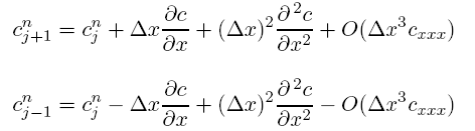
Substituting (5.4.1) and (5.4.2) into (5.3.21) and keeping all the terms up to second derivatives we find that we are actually solving the equation

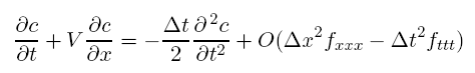
To make this equation a bit more familiar looking, it is useful to transform the time derivatives into space derivatives. If we take another time derivative of the original equation (with constant V) we get

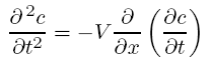
and substituting in the original equation for δc/δt we get

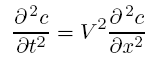
Thus Eq. (5.4.4) becomes

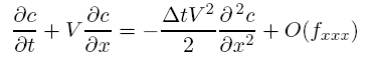
But this is just an advection-diffusion equation with effective diffusivity κ_eff =−∆tV²/2. Unfortunately, for any positive time step ∆t > 0 the diffusivity is negative which is a physical no-no as it means that small perturbations will gather lint with time until they explode (see figure 5.3). This negative diffusion also accounts for why the initial gaussian actually narrows and grows with time. Thus the FTCS scheme is unconditionally unstable.

Схема чехарды

The staggered leap frog scheme uses a 2nd ordered centered difference for both the time and space step. i.e. our simplest advection equation (5.2.2) is approximated as

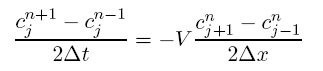
or as an updating scheme

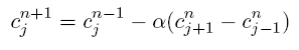
which superficially resembles the FTCS scheme but is now a two-level scheme where we calculate spatial differences at time n but update from time n − 1. Thus we need to store even and odd time steps separately. Numerical Recipes gives a good graphical description of the updating scheme and shows how the even and odd grid points (and grids) are decoupled in a “checkerboard” pattern (which can lead to numerical difficulties). This pattern is where the “staggered-leapfrog” gets its name.

While the staggered-leapfrog scheme is non-diffusive (like our original equation) it can be dispersive at high frequencies and small values of α. If we do a Hirt’s stability analysis on this scheme we get an effective differential equation

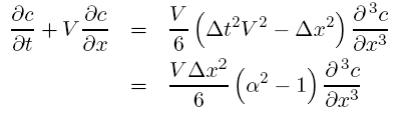
which is dispersive except when α = 1. Unfortunately since α is defined for the maximum velocity in the grid, most regions usually (and should) have α < 1. For well resolved features and reasonable Courant numbers, the dispersion is small. However, high frequency features and excessively small time steps can lead to more noticeable wiggles. Figure 5.5 shows a few examples of dispersion for α =.5 and α =.5 but for a narrower gaussian. In both runs the gaussian travels around the grid 10 times (t_max = 100) (for α = 1 you can’t tell that anything has changed).

For many problems a little bit of dispersion will not be important although the wiggles can be annoying looking on a contour plot. If however the small negative values produced by the wiggles will feed back in dangerous ways into your solution you will need a non-dispersive scheme. The most commonly occuring schemes are known as upwind schemes. Before we develop the standard upwind differencing and a iterative improvement on it, however it is useful to develop a slightly different approach to differencing.

Дата добавления: 2014-01-04