Другие комбинации и схемы более высокого порядка точности

In Eq. (5.3.1) we considered the value of our function at one grid point forward in ∆x. We could just have easily taken a step backwards to get

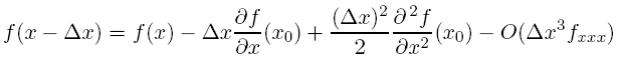
If we truncate at order ∆x² and above we still get a first order approximation for the Backward space step (BS)

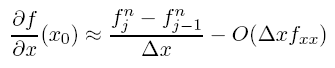
which isn’t really any better than the forward step as it has the same order error (but of opposite sign). We can do a fair bit better however if we combine Eqs. (5.3.1) and (5.3.5) to remove the equal but opposite 2nd order terms. If we subtract (5.3.5) from (5.3.1) and rearrange, we can get the centered space (CS) approximation

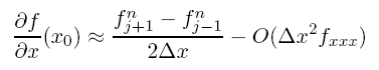
Note we have still only used two grid points to approximate the derivative but have gained an order in the truncation error. By including more and more neighboring points, even higher order schemes can be dreamt up (much like the 4th order Runge Kutta ODE scheme), however, the problem of dealing with large patches of points can become bothersome, particularly at boundaries. By the way, we don’t have to stop at the first derivative but we can also come up with approximations for the second derivative (which we will need shortly). This time, by adding (5.3.1) and (5.3.5) and rearranging we get

This form only needs a point and its two nearest neighbours. Note that while the truncation error is of order ∆x² it is actually a 3rd order scheme because a cubic polynomial would satisfy it exactly (i.e. f_xxxx = 0).

Направленная вперед по времени центральная по пространству схема

I will show you a simple, easily coded and totally unstable technique known as forward-time centered space or simply the FTCS method. If we consider the canonical 1-D transport equation with constant velocities (5.2.2) and replace the time derivative with a FT approximation and the space derivative as a CS approximation we can write the finite difference approximation as

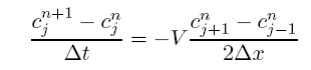
or rearranging for cn+1 j we get the simple updating scheme

where

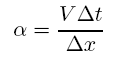
is the Courant number which is simply the number of grid points traveled in a single time step.

Дата добавления: 2014-01-04