Численные методы решения уравнения адвекции

Основной идеей конечно-разностных, сеточных методов является наложение статической сетки на область решений и аппроксимация частных производных в каждой точке этой сетки. Стандартный подход для аппроксимации частных производных исходит из рядов Тейлора. Рассмотрим функцию f(x, t ) в фиксированный момент времени t. Если f непрерывна в пространстве, то мы можем разложить ее в окрестностях любой точки f(x + ∆x) в ряд Тейлора

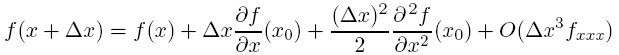
где индекс x означает частную производную по x. Если пренебречь членами ряда порядка ∆x² и больше, то мы можем проаппроксимировать первую производную в любой точке x₀ в виде

If we consider our function is now stored in a discrete array of points f_j and x = ∆x_j where ∆x is the grid spacing, then at time step n we can write the forward space or FS derivative as

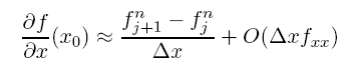
An identical procedure but expanding in time gives the forward time derivative (FT) as

Both of these approximations however are only first order accurate as the leading term in the truncation error is of order ∆x or ∆t. More importantly, this approximation will only be exact for piecewise linear functions where f_xx or f_tt = 0.

Дата добавления: 2014-01-04