Основы графического метода в термодинамике

Расчет работы в технической термодинамике.

В терминологии лекции 1 работа внешней среды над рабочим телом – это просто количество деформационного воздействия dw = pdv. Причем, ранее показано, что dw не является полным дифференциалом и что величина

(2.22)

сильно зависит не только от параметров начального и конечного состояния в точках 1 и 2 процесса, но и от его траектории.

Если известно уравнение связи p = p(v), то расчет количества работы сводится ко взятию интеграла в (2.22). В технической термодинамике эта связь давления и удельного объема чаще всего представляется в виде:

pvⁿ = const или pvⁿ = p₁v₁ⁿ, т.е. p = p₁v₁ⁿv^-n, при n = const. (2.23)

Это уравнение в технической термодинамике носит название политропы – каждое значение n определяет свою «тропу», т.е. траекторию, и отражает связи параметров p и v. Подробнее о политропах будем говорить в лекции 3.

Если подставить эту зависимость p = p(v) в (2.22), то получим табличный интеграл, который после несложных преобразований с помощью (2.23) приводится к одному из следующих видов:

или 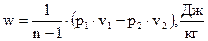. (2.24)

Расчетные формулы (2.24) пригодны для политропического процесса для любого реального вещества.

Для идеального газа с учетом связи pv = R_уT расчетная формула в (2.24) несколько упрощается:

(2.25)

Полная работа деформации (сжатия или расширения) за процесс рассчитывается как:

W = mw, Дж, где m – масса рабочего тела.

Если зависимость p = р(v) представлена в графическом виде, т.е. процесс с рабочим телом изображен на диаграмме p – v для какого-то вещества, то расчет количества работы можно провести в соответствии с рис. 2.4, как площадь под линией процесса до оси v.

Расчет количества работы возможен с помощью первого закона термодинамики:

Δu = q – w → w = q – Δu, (2.26)

если предварительно найти изменение внутренней энергии Δu и количество теплоты q так, как показано в этой лекции выше.

Замечание. В этом параграфе до сих пор шла речь о работе деформации рабочего тела, т.е. сжатия или расширения термодинамической системы в геометрическом пространстве. Однако, в технической термодинамике необходимо уметь рассчитывать работу проталкивания:

dw΄ = vdp, Дж/кг (2.27)

Особенно, этот расчет необходим для проектирования компрессоров и для определения мощности их привода. В этом случае (2.27) называют располагаемой работой.

На рис. 2.10 представлены две диаграммы в осях p – V теоретическая рабочая и p – v термодинамическая для процесса компремирования. Для идеального одноступенчатого компрессора этот процесс состоит из двух изобар и одной политропы с заданным показателем n.

Рис. 2.10. Иллюстрация работы компрессора в диаграммах p – V и p – v.

Процесс 0 – 1 – всасывание исходной газовой среды, процесс 1 – 2 –

сжатие, 2 – 3 – проталкивание сжатого газа потребителю.

Площадь слева от кривой процесса сжатия pvⁿ = const и представляет собой затраченную на сжатие газа работу (располагаемая работа):

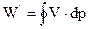. Дж.

Можно перейти к удельному объему v от геометрического V, если уделить последний на все количество газа m, вошедшего в цилиндр компрессора за весь процесс всасывания 0 – 1. Тогда техническая работа компрессора равна

Дж/кг. (2.28)

Снова воспользуемся уравнением политропы:

pvⁿ = const → pvⁿ = p₁v₁ⁿ → v = v₁p₁^1/n p^-1/n (2.29)

и подставим полученную зависимость v = v(p) в интеграл (2.28). Опять получается табличный интеграл, после преобразования результата интегрирования с помощью (2.29) окончательно приходим к равенству:

w΄ = nw, где w рассчитывается по (2.24) или (2.25).

Иными словами, работа, затраченная на компрессию газа (располагаемая) в n раз больше работы простого сжатия.

Мощность двигателя для привода одноступенчатого идеального компрессора рассчитывается как:

N_двиг = Gw΄/η, Вт, (2.30)

где G – массовый расход сжимаемого газа, кг/с, η – коэффициент полезного действия привода.

Замечание. В инженерной практике и, следовательно, в технической термодинамике приходится рассматривать процесс проталкивания газов через каналы, сопла (реактивные двигатели, газовые и паровые турбины). Линейные скорости течения газов в таких каналах настолько велики (звуковые и сверхзвуковые скорости), что процесс течения газа можно рассматривать как адиабатический (нет теплообмена). Это означает, что без учета трения потока газа о стенки канала и трения в самом потоке – s = const, ds = 0. В этой ситуации работа проталкивания рассчитывается через функцию состояния – энтальпию (2.5):

dh = Tds + vdp → dh = vdp → w΄ = 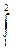dh = Δh = h₂ – h₁.

Здесь для идеального газа справедливо выражение (2.20), а для реального рабочего тела используются расчетные таблицы свойств веществ (например, «Таблицы состояния аммиака», «Таблицы для воды и водяного пара» и т.д.).

5.1. p – v диаграмма.

На рис. 2.8 представлены графики зависимости pv=R_уT для различных изопроцессов: показан ход изобары (p = const), изохоры (v = const), изотермы (pv = const), изоэнтропы (pv^k = const) для идеального газа. По построению в p – v координатах две линии – прямые (p и v), одна (T = const) – равнобокая гипербола и неравнобокая – изоэнтропа (s = const) pv^k = const.

Такой график удобен для качественного анализа изменения параметров и функций процессов. Для точных расчетов не используется.

Рис. 2.8 Графики зависимостей р от v для различных изопроцессов p, v, T, s = const с

рабочим телом в состоянии идеального газа.

5.2. T – s диаграмма.

Рассмотрим ход кривых p = const и v = const в диаграмме с координатами T – s. В термодинамике количество термического воздействия (теплоты) рассчитывается как dq = Tds, а в калориметрии – как dq = cdT. Отсюда

Tds = cdT → ds = cdT/T → s₂ –s₁ = 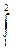[c_x(T)/T] dT = 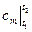ln T₂/T₁.

Расчетную формулу для приращения энтропии Δs получим из с_х|^t2_t1 при х = р или х =v:

Δs = 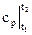lnT₂/T₁ для p = const и Δs = 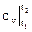lnT₂/T₁ для v = const. (2.31)

Окончательно,

T₂ = T₁exp{(s –s₀)/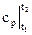} и T₂ = T₁exp{(s –s₀)/}.

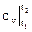Таким образом, изобара и изохора в осях T – s являются обычными экспонентами, причем из-за того, что с_р > c_v, изохора круче изобары (см. рис. 2.9), т.к. dT/ds = T/c – тангенс угла касательной к графику соответствующей кривой.

Рис. 2.9. Взаимное расположение графиков процессов

p = const и v = const в осях (Ts), так как c_p > c_v то изохора проходит круче изобары.

Здесь же показаны процессы s = const и Т = const.

В поле графика T – s (см. рис. 2.9) прямые линии T = const и s = const при избранных масштабах температур и условных значений энтропии (отсчет от s₀ = 0 в избранном масштабе), а так же экспоненты p = conct и v = const образуют сетку энтропийной (тепловой) диаграммы.

Возможно использование оси ординат для нанесения условного значения энтальпии от h₀ = 0: h = c_р|^t₀*t кДж/кг. Такая диаграмма удобна для широко распространенных изобарных и изоэнтропийных процессов. В первом случае (p = const) dh = Tds + vdp, т.е. h = ∫Tds = q_p. Во втором (s = const) dh = Tds + vdp, т.е. h = ∫vdp – работа компрессора.

Для инженерной практики теплофизические институты создают диаграммы p – v и T – s для различных веществ и рабочих тел. Использование их существенно ускоряет расчетный процесс, если не требуется особенная точность.

Дата добавления: 2014-01-04