Уравнение процесса

Политропный процесс.

Этапы термодинамического расчета процессов.

Термодинамический расчет процессов.

Термодинамика. Лекция 3.

К.т.н. Прохоренко Н.Н.

Определение. Процессом называется непрерывная смена состояний рабочего тела.

Термодинамический расчет подобного физического изменения состояний является в сущности приложением выработанного в предыдущих лекциях термодинамического аппарата к инженерным и научно-техническим задачам. Физика обработки технологических потоков в химических технологиях при их различных фазовых состояниях безусловно влияет на методику расчета.

Замечание. Часто в инженерии используется термин «газ» и нередко термин «пар». Каково происхождение этих терминов и их соотношение? Исторически (в средние века) вещество называли газом, если не могли (по техническим причинам или по неведению) получить его в жидком состоянии. А если могли, то называли паром. Поэтому в те времена воздух называли газом, а Н₂О в газообразном состоянии – паром. Сейчас проблема ожижения любого газа (и вещества), даже перевод его в твердое состояние, решена. Студентам следует относиться к словам «газ» и «пар» какого-то вещества в определенном состоянии как к синонимам.

Цель расчета процесса: определение исходных данных для создания технологии или расчета, оптимизации и выбора аппарата или машины.

1. До численного решения установить термодинамические особенности процесса (постоянство какого-то параметра или отсутствие какого-то взаимодействия с внешней средой). Иными словами, определить инварианты процесса.

2. Найти уравнение процесса.

3. Получить связь между параметрами состояния (p, v, T,s) рабочего тела для двух произвольных состояний процесса.

4. Рассчитать изменение функций состояния Δu, Δh и изменение энтропии Δs, рассчитать количества внешних воздействий (функций процесса q, w).

5. Изобразить процесс в термодинамической системе координат p – v, T – s, h – s.

В этой лекции мы в основном сосредоточимся на реализации этапов и порядка расчетов по виду (по особенностям) процесса, а не по свойствам рабочего тела.

В лекции 2 довольно кратко уже говорилось о политропе, теперь – подробнее.

Уравнение политропического процесса имеет вид:

pvⁿ = const, n = const.

Но это не единственная форма связи параметров состояния, возможны комбинации:

pT^n΄ = const, n΄ = const или vT^n΄΄= const, n΄΄= const.

Далее, для примера, будем работать с уравнением pvⁿ = const, n = const.

На практике показатель политропы n находят экспериментально следующим образом:

pvⁿ = const → lnp + nlnv = const → lnp = - nlnv + const.

Последнее выражение представляет собой уравнение прямой линии в координатах lnp – lnv. В эксперименте с каким-то веществом для различных условий измеряют давление р и удельный объем v с какой-то инструментальной точностью. Далее строят график в осях lnp – lnv (см. рис. 3. 1) и по нему находят показатель политропы n.

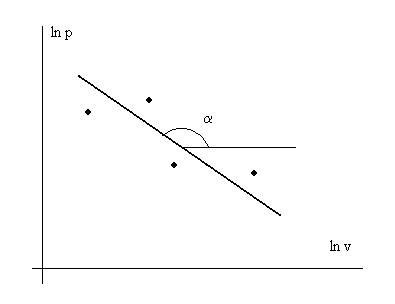
Рис. 3. 1. Иллюстрация к экспериментальному определению

показателя политропы n – индикаторная диаграмма

в логарифмических координатах. n = - tgα.

· - обозначение экспериментальных точек.

Истоки вывода уравнения pvⁿ = const уходят в анализ работы реальных поршневых машин (паровых и компрессоров). При анализе их работы снимали индикаторную диаграмму p = f(x), где х – ход поршня. От индикаторной диаграммы всего один шаг до p – v диаграммы.

Показатель политропы n в уравнении pvⁿ = const в сущности отражает интенсивность изменения параметров в процессе, т.е. характер смены состояний. А параметры изменяются под влиянием внешних воздействий q и w на термодеформационную систему. Поэтому мы в праве ожидать, что n = n(q,w). Проверим это ожидание.

Исходное уравнение политропы pvⁿ = const в логарифмической форме

lnp = -nlnv + const

после дифференцирования принимает вид:

dp/p = -n dv/v или n = -vdp/pdv (3.1)

Иными словами: показатель политропы n есть отношение элементарной работы проталкивания к элементарной работе деформации (сжатия или расширения), и наши ожидания подтвердились.

Далее, вспомним первый закон термодинамики в форме

du = dq – dw → du = dq – pdv → pdv = dq – du; (3.2.1)

dh = dq +dw΄ → dh = dq +vdp → vdp = dh – dq; (3.2.2)

Подстановка (3.2.1) и (3.2.2) в (3.1) дает результат:

n = (dq – dh) / (dq –du). (3.3)

В лекции 2 подробно рассматривалось понятие теплоемкости и было показано, что dq = cdT. Одновременно, для идеального газа и любого процесса были получены связи

du = c_vdT и dh = c_pdT.

Тогда зависимость (3.3) для идеального газа принимает вид:

n = (cdT – c_pdT) / (cdT – c_vdT) = (c – c_p)/(c – c_v). (3.4)

Следовательно, показатель политропы n для идеального газа получил вполне определенный смысл – это функция теплоемкостей.

Из (3.4) попутно получим зависимость истинной политропной теплоемкости с_n от показателя политропы n, чтобы можно было рассчитывать количество теплоты так, как это принято в калориметрии dq = c_ndT. Действительно (см. (3.4)),

c ≡ c_n = (nc_v –c_p) / (n – 1) = c_v (n – k) / (n – 1). (3.5)

В (3.5) величина k ≡ с_р/с_v носит название коэффициента Пуассона и является показателем адиабаты. Для двухатомных газов k ≈ 1,4. Так как n = const и k = const, то (3.5) справедливо и для средней политропной теплоемкости:

c_n|_t1^t2 = c_v|_t1^t2(n – k) / (n – 1), k = c_p|_t1^t2 / c_v|_t1^t2. (3.6)

Дата добавления: 2014-01-04