
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейная независимость собственных векторов, имеющих попарно-различные собственные значения
|
|
|
|
Существование одномерных и двумерных инвариантных подпространств
Теорема 51.3: Линейная оболочка, натянутая на собственный вектор x, соответствующий собственному значению λ линейного оператора  , является инвариантным подпространством линейного оператора
, является инвариантным подпространством линейного оператора  .
.
Доказательство:
Для любого 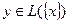 имеем y=αx при некотором α. Тогда
имеем y=αx при некотором α. Тогда  , то есть
, то есть 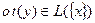 и теорема 51.3 доказана.
и теорема 51.3 доказана.
А так как степень характеристического многочлена P(x) совпадает с размерностью всего линейного пространства, то имеет место следующая теорема:
Теорема 51.4: Всякий линейный оператор  в линейном пространстве нечётной размерности имеет инвариантное одномерное подпространство (являющееся линейной оболочкой собственного вектора x, соответствующее собственному значению λ - вещественному корню характеристического многочлена линейного оператора
в линейном пространстве нечётной размерности имеет инвариантное одномерное подпространство (являющееся линейной оболочкой собственного вектора x, соответствующее собственному значению λ - вещественному корню характеристического многочлена линейного оператора  ).
).
( - мнимая единица, т.е
- мнимая единица, т.е 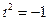 )
)
Пусть теперь - комплексный корень характеристического многочлена. Перейдя к матричной форме записи, получим, что система линейных уравнений (51.2) должна иметь комплексное ненулевое решение z=x+yj, или (A - вещественная матрица, ибо
- комплексный корень характеристического многочлена. Перейдя к матричной форме записи, получим, что система линейных уравнений (51.2) должна иметь комплексное ненулевое решение z=x+yj, или (A - вещественная матрица, ибо 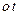 - вещественный линейный оператор):
- вещественный линейный оператор):
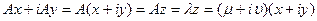 (51.4)
(51.4)
Раскроем в (51.4) скобки: 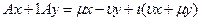
Сравнивая вещественные и мнимые части обеих частей последнего равенства, имеем
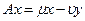 и
и 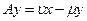 (51.5)
(51.5)
или, переходя к линейному оператору 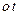 и полагая
и полагая 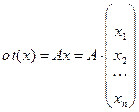 (см. (50.2)) ранее выбранный базис, получим:
(см. (50.2)) ранее выбранный базис, получим:
 и
и 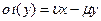 (51.6)
(51.6)
Берем теперь любое 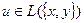 ,то есть
,то есть 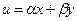 при некоторых α и β. Тогда:
при некоторых α и β. Тогда: 
то есть L({x;y} (являющееся двумерным линейным подпространством) – инвариантное подпространство линейного оператора 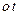 . Таким образом, доказана следующая теорема:
. Таким образом, доказана следующая теорема:
Теорема 51.5: Всякий линейный оператор  имеет одномерное или двумерное инвариантное подпространство.
имеет одномерное или двумерное инвариантное подпространство.
Покажем, что имеет место следующая теорема:
Теорема 51.6: Если собственные значения  линейного оператора
линейного оператора  попарно различны, то соответствующие им собственные вектора
попарно различны, то соответствующие им собственные вектора 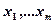 линейно независимы.
линейно независимы.
Доказательство:
Используем метод математической индукции по числу собственных значений m:
1. База индукции: m=1
Так как собственный вектор x≠0, то система {x} линейно независима (см. §16, теорема 16.0).
2. Шаг индукции: 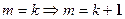
Имеем: вектора 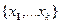 линейно независимы (попарно различные собственные значения -
линейно независимы (попарно различные собственные значения -  ; соответствующие им собственные вектора -
; соответствующие им собственные вектора - 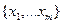 ).
).
Рассмотрим произвольную линейную комбинацию для собственных векторов 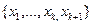
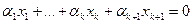
(51.7)
Тогда 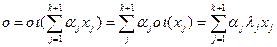
то есть доказано равенство
 (51.8)
(51.8)
Умножая обе части (51.7) на λk+1 и вычитая полученное равенство из (51.8), имеем
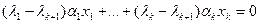 (51.9)
(51.9)
А так как система 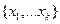 линейно независима по индуктивному предположению, то
линейно независима по индуктивному предположению, то
 (51.10)
(51.10)
Ввиду того, что 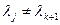 (то есть
(то есть  ) для любых j=1,…k (собственные значения
) для любых j=1,…k (собственные значения  попарно различны), из равенства (51.10) получаем, что
попарно различны), из равенства (51.10) получаем, что
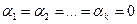 (51.11)
(51.11)
Подставляя вместо 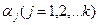 в (51.7) их значения из (51.11), получим, что
в (51.7) их значения из (51.11), получим, что 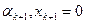 , а так как
, а так как  , то из теоремы 16.0 имеем
, то из теоремы 16.0 имеем  , то есть (см. (51.11):
, то есть (см. (51.11): 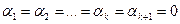 , и, следовательно, система линейно независима (ибо мы показали, что равенство (51.7) может выполняться только при нулевых значениях
, и, следовательно, система линейно независима (ибо мы показали, что равенство (51.7) может выполняться только при нулевых значениях 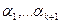 ). Теорема 51.6 доказана.
). Теорема 51.6 доказана.
Простым следствием теоремы 51.6 является следующая теорема:
Теорема 51.7: Если все корни характеристического многочлена 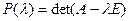 линейного оператора
линейного оператора  действительные и простые (попарно различные), то в линейном пространстве имеется базис из собственных векторов линейного оператора
действительные и простые (попарно различные), то в линейном пространстве имеется базис из собственных векторов линейного оператора  .
.
Рассмотрим матрицу линейного оператора  в базисе его собственных векторов:
в базисе его собственных векторов:
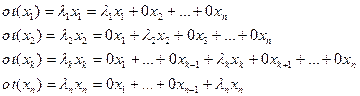
то есть эта матрица имеет вид:
и является диагональной матрицей.
Итак, доказаны следующие две теоремы:
Теорема 51.8: Матрица линейного оператора  в базисе его собственных векторов является диагональной.
в базисе его собственных векторов является диагональной.
Теорема 51.9: Если уравнение
 (51.12)
(51.12)
Имеет вещественные простые (попарно различные) корни, то существует такая невырожденная матрица C, что C-1∙A∙C является диагональной матрицей.
Эта матрица C будет матрицей перехода к базису из собственных векторов линейного оператора  соответствующих собственным значением
соответствующих собственным значением 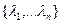 , являющихся корнями уравнения (51.12).
, являющихся корнями уравнения (51.12).
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2432; Нарушение авторских прав?; Мы поможем в написании вашей работы!