Квадратичная форма как симметричный билинейный функционал

Квадратичную форму можно определить как БФ от одного и того же элемента, т.е. а 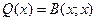. Проведем вычисления; согласно формуле (53.1), где мы 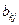заменили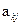

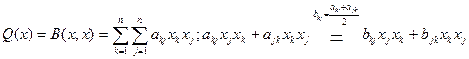и тогда

(53.2), где 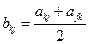- элемент некой симметричной матрицы 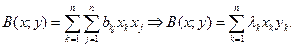существует такой ОНБ, в котором матрица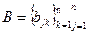 - диагональная т.е имеет вид ;

Здесь будет 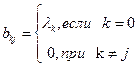(53.3)

Подставляя вместо 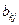в формулу (53.2) его значение из равенства (53.3), в этом базисе получим:

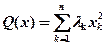(53.4)

Определение: Равенство (53.4) является каноническим видом квадратичной формы Q(x).

В качестве частного случая теоремы 53.2 рассмотрим квадратную форму в трехмерном пространстве.

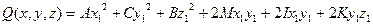
Ее каноническим видом (в базисе собственных векторов СЛО, задавались матрицей 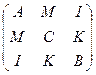) будет: 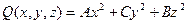и поверхность, задаваемая уравнением (47.1) в этом базисе принимает уравнение (47.3). Теорема, сформулированная в начале §47 доказана.

Наконец доказана теорема53.2: Для всякой квадратичной формы ОНБ, в котором она имеет канонический вид.

Заключение

Наконец-то Вы прослушали курс или прочитали вышеизложенный учебник. Сейчас пойдёт речь о предстоящем у Вас экзамене.

Прежде всего, придерживайтесь не столько вышеизложенного (да и какого-либо иного) учебника, сколько того курса лекций, который был Вам прочитан. Как правило, на своих лекциях я читаю большую (но далеко не всегда всю) часть вышеизложенного материала.

В общем случае весь вышеизложенный курс с полными выводами и доказательствами всех теорем за 18 лекций изложить невозможно. К тому же некоторые лекции могут прийтись и на праздничный день; возможна и иная причина отмены лекции. Поэтому, согласно с особенностями расписания занятий, каждый год в программу курса вносятся некоторые коррективы. Естественно, что наиболее «страдающей» частью по коррективам оказывается последняя (пятая)глава.

Вообще-то полностью вышеизложенный куре я смог прочитать лишь 1 (один) раз - в 2003 году в потоке 3C030I, 0C030I, когда у всех студентов данного потока я вёл практические занятия, и в обеих группах вместо двух практических занятий я читал лекции. И только за счёт этих двух дополнительных лекций я смог этот курс прочитать до конца. При этом четыре студента этого потока (точнее - группы 0C030I) - В.Ю. Федосеенков, А.К. Чичкан, В.Э. Журавлёв и И.Е. Власов со своих конс­пектов начали составлять данный учебник в электронном виде (каждый из них набирал одну или две главы данного курса).

Естественно, что основное внимание было уделено пятой главе, которую, как я уже говорил выше, полностью удалось прочитать в их потоке в их год обучения.

Основу данного электронного курса (практически без трехмерных чертежей и рисунков) составили три студента следующего года обучения: С.В.Захаров, А.С. Бабий, Д.Д. Васильев. Они в частности ввели соответствующие пункты в заключение данного курса, а так же более подробно, используя методы математического анализа (это относиться к их «руководителю» С.В. Захарову), исследовали поведение кривых второго порядка (на лекциях, за неимением времени, я это не провожу, и поэтому всем трем вышеперечисленным студентам группы ПС0402, а в особенности С.В. Захарову, я весьма признателен)

Трехмерные чертежи поверхности первого порядка составляли студенты следующего (2005) года обучения: И.Ю.Карташов, А.А.Макаров, А.В. Дорофеев, П.И.Пухов (все из группы СС0505). Они так же, с учетом моих замечаний, устраняли некоторые из предыдущих недоделок, а так же соединили почти весь курс, кроме пяти параграфов) в единый текст.

Черчение поверхностей второго порядка сделали двое студентов 2006 года обучения: Н.Г.Сергеев и П.В. Осипов. (Оба из группы КТ0601). Они, с учетом моих замечаний, довели данный электронный курс до конца.

Всем тринадцати вышеперечисленным студентам я (да, наверное, и Вы, дорогой читатель) очень благодарен.

Как я уже говорил выше, последнюю главу удается прочитать крайне редко, и поэтому

экзаменационные билеты составлены по "наихудшему" варианту - тео­рем и выводов пятой главы они не содержат. И для проставления удовлетворительной оценки пятую главу я и не спрашиваю. Для проставления же хорошей и, тем более, отличной оценкой я уже спрашивай все те теоремы и выводы последней главы (да и всех остальных глав), которые мной были прочитаны, причём для отличной оценки – их полные выводы (даже для последней главы - общий критерий доставления оценок я приведу ниже) и умение их применить при решении оригинальных задач.

Отметим также, что оценки проставляются за знание всего данного курса, а не какой-либо его части и соответствуют не широте, а глубине усвоения Вами материала.

Перейдём теперь к критериям проставления оценок.

Дата добавления: 2014-01-04